3 . fejezet Deskriptív statisztika

Ebben az fejezetben a statisztika deskriptív ágával fogunk foglalkozni. Már utaltunk rá, hogy deskriptív statisztikáról akkor beszélünk, amikor kizárólag a mintában lévő információt igyekszünk valamilyen módon megragadni (és nem törődünk azzal, hogy a minta maga is csak a valóság egy ,,szelete’’, szebben megfogalmazva: figyelmen kívül hagyjuk a mintavételi helyzetet).

Először ezt a gondolatot fogjuk pontosítani, közelebbről körüljárni; majd pedig megismerkedünk a leíró statisztika legalapvetőbb módszereivel. Látni fogunk grafikus és analitikus módszereket, foglalkozunk egy- és (röviden) többváltozós helyzetekkel; az ismertetést pedig a vizsgált változók mérési skálája (@ref{alapokvaltozok}. alfejezet) szerint végezzük. (Azzal, hogy a nominális és az ordinális, illetve az intervallum- és arányskálán mért változókat nem választjuk szét, hanem minőségi és mennyiségi változókról fogunk beszélni.) Ezek után az olvasó számára ismerős lesz a mai orvostudományi cikkekben alkalmazott deskriptív eszköztár túlnyomó része; az elemi eszközöknek pedig szinte egésze.

Ebben a fejezetben a már említett módon a Low Infant Birth Weight adatbázist fogjuk futó példaként használni a módszertani mondanivaló illusztrálására. Az ábrák és a számítások statisztikai környezet alatt készültek.

3.1 A deskriptív statisztikáról általában

Amint már többször említettük, a deskriptív statisztika definíciós jellemzője, hogy kizárólag a mintában lévő információval törődik, számára az az ,,univerzum’, és teljes mértékben figyelmen kívül hagyja azt a kérdéskört, hogy a mintában lévő információ hogyan viszonyul a sokaságban lévő információhoz. Innen ered a módszer neve is: a deskripció leírást jelent, azaz a deskriptív módszerek pusztán a minta – valamilyen szempontból ,,jó’ – leírását célozzák meg (nem pedig következtetést a sokaságra). Nem véletlen, hogy ebben a kontextusban nagyon sokszor minta helyett adatbázist mondunk (tükrözve, hogy itt igazából nincs is jelentősége annak, hogy az adataink csak – a szó statisztikai értelmében – egy mintát jelentenek).

A ,,jó leírás’’ alatt legtöbbször azt értjük, hogy a mintában lévő információt úgy próbáljuk tömöríteni, hogy közben – valamilyen elemzési célra tekintettel – kiemeljük a lényeget. Erre azért van szükség, mert a legtöbb esetben a mintában lévő információ (még ha csak néhány változóra, és néhány tucat megfigyelési egységre is gondolunk) feldolgozhatatlan ,,ránézésre’. A számok tengeréből még a legalapvetőbb kérdésekre sem tudnánk válaszolni. Szükség van tehát olyan módszerekre, melyek ,,emészthetővé teszik’ ezt a számtengert: csökkentik a bonyolultságát, hogy tudjuk értelmezni azt, fel tudjuk használni kérdések megválaszolásához, illetve új megállapítások eléréséhez.

Nyilvánvaló, hogy a bonyolultság csökkentése csak úgy lehetséges, ha információt hagyunk el. Az egész művelet kritikus pontja épp ez: annak megválasztása, hogy mennyi információt hanyagoljunk el (és persze hogyan). A ,,hogyan’’ szerepe triviális: ha egy adott, mennyiségi változóra vonatkozó 100 elemű mintából elhagyjuk az első 99 elemet, akkor ugyan egyetlen számmá, azaz teljesen áttekinthetővé alakítjuk az információt – csak épp nyilván semmit nem érünk el vele. Ha viszont kiszámoljuk az átlagot, akkor ugyanúgy egyetlen számot kapunk, de immár úgy, hogy annak van értelme, azaz felhasználhatjuk kérdések megválaszolásához, illetve új megállapítások eléréséhez.

A meghatározó kulcskérdés az elhanyagolásban (az információtömörítésben) tehát a ,,mennyit’’. Látható, hogy trade-off áll fenn az áttekinthetőség, és a reprodukciós hűség között: minél többet hanyagolunk el, annál inkább segítjük az áttekinthetőséget, de annál többet vesztünk az eredeti információ hűséges reprodukciójából. A deskriptív statisztika igazi sava-borsa (végeredményben a legtöbb módszer, így vagy úgy, de ebben foglal el egy álláspontot) a jó kompromisszum megkötése a kettő között. Példának okáért, adatbázisunkban a születési tömeg változó megfigyelései így néznek ki:

birthwt$bwt

##   [1] 2523 2551 2557 2594 2600 2622 2637 2637 2663 2665 2722 2733 2751 2750 2769
##  [16] 2769 2778 2782 2807 2821 2835 2835 2836 2863 2877 2877 2906 2920 2920 2920
##  [31] 2920 2948 2948 2977 2977 2977 2977 2922 3005 3033 3042 3062 3062 3062 3062
##  [46] 3062 3080 3090 3090 3090 3100 3104 3132 3147 3175 3175 3203 3203 3203 3225
##  [61] 3225 3232 3232 3234 3260 3274 3274 3303 3317 3317 3317 3321 3331 3374 3374
##  [76] 3402 3416 3430 3444 3459 3460 3473 3544 3487 3544 3572 3572 3586 3600 3614
##  [91] 3614 3629 3629 3637 3643 3651 3651 3651 3651 3699 3728 3756 3770 3770 3770
## [106] 3790 3799 3827 3856 3860 3860 3884 3884 3912 3940 3941 3941 3969 3983 3997
## [121] 3997 4054 4054 4111 4153 4167 4174 4238 4593 4990  709 1021 1135 1330 1474
## [136] 1588 1588 1701 1729 1790 1818 1885 1893 1899 1928 1928 1928 1936 1970 2055
## [151] 2055 2082 2084 2084 2100 2125 2126 2187 2187 2211 2225 2240 2240 2282 2296
## [166] 2296 2301 2325 2353 2353 2367 2381 2381 2381 2410 2410 2410 2414 2424 2438
## [181] 2442 2450 2466 2466 2466 2495 2495 2495 2495

Ezt a megadást nevezhetnénk az egyik végpontnak ebben a kompromisszumban: 100% reprodukciós hűség, de – szinte – 0% áttekinthetőség. Ez a legalapvetőbb kérdések megválaszolását, a legalapvetőbb észrevételek elérését is lehetetlenné teszi.

Másik végpontnak vehetjük azt, amikor a fenti adatoknak csak az átlagát adjuk meg 2944.5873016.

Ez 0%-hoz közeli reprodukciós hűséget jelent (189 számból 1-et ,,gyártottunk’’, szinte semmit nem tudunk reprodukálni az eredeti adatbázisból), viszont remek az áttekinthetősége (például azonnal látható, hogy milyen érték körül csoportosulnak az adatok).

Az igazán érdekes az, hogy – természetszerűleg – a két végpont között számos egyéb kompromisszumot köthetünk. Megadhatjuk például (az utóbbi végponttól az előbbi felé haladva) az adatok átlagát és szórását: 2944.5873016 $\pm$ 729.2142952, az adatok átlagát, mediánját, szórását és interkvartilis terjedelmét³: 2944.5873016 (2977) $\pm$ 729.2142952 (1073), vagy épp az adatok átlagát, mediánját, szórását, interkvartilis terjedelmét, illetve minimumát és maximumát: 2944.5873016 (2977) $\pm$ 729.2142952 (1073) [709-4990].

Látszik, hogy minden ilyen megadás egyfajta kompromisszum: egyre több információt őrzünk meg (egyre kevesebb az adatvesztés, hűségesebb a reprodukció), viszont közben romlik a megadás áttekinthetősége.

Összefoglalva tehát megállapíthatjuk, hogy bár az információtömörítés ugyan szükségképp adatvesztést jelent, ez azonban nem feltétlenül baj, épp ellenkezőleg: ez teszi lehetővé, hogy a fontosat észrevegyük. A kulcs a kettő közötti egyensúlyozás.

3.2 A deskriptív statisztika módszereinek csoportosításáról

Azért, hogy az igen nagy számú leíró statisztikai módszert áttekinthetően tudjuk tárgyalni, érdemes megismerkedni pár szemponttal, melyek mentén e módszerek jellegzetes, és gyakorlati szempontból fontos csoportokba sorolhatóak.

3.2.1 Grafikus és analitikus módszerek

A fent mutatott példák (átlagtól szóráson át a terjedelemig) mind ún. analitikus eszközök voltak, azaz a (számszerű) információból számszerű, csak épp tömörebb, lényeget kiemelő információt gyártottak. Az analitikus módszerek tipikus példái a mutatószámok, mint amilyen az átlag vagy a szórás, bár léteznek ennél komplexebb (nem egyetlen számból álló) eredményt szolgáltató analitikus eszközök is – az azonban közös pont, hogy mindegyik számszerű kimenetet ad.

Ezzel állnak szemben a grafikus módszerek, melyek a bemenő (számszerű) információból valamilyen képi megjelenítést konstruálnak. Szokás ezért az ilyet adatvizualizációnak is nevezni, bár ezt a megnevezést gyakran csak a komplexebb módszerekre alkalmazzák.

A grafikus módszerek általában kevésbé tömörek és kevésbé objektivizálhatóak (ami gond lehet, ha például összehasonlításra van szükség), de cserébe nagyon sokszor jobban értelmezhető benyomást tudnak adni a vizsgált adatbázisról. Ennek hátterében az van, hogy az emberi agy különösen alkalmas struktúrák azonosítására, vizsgálatára grafikus információkban; így ha ügyesen tudjuk vizualizálni adatbázisunk tartalmát, azzal nagyban megkönnyíthetjük az elemzését. Nem véletlen, hogy John Wilder Tukey egyszer azt mondta: ``There is no excuse for failing to plot and look!’’ (,,Nincs mentség arra, ha nem ábrázoljuk az adatokat és nézünk egyszerűen rá!’’).

3.2.2 Egy- és többváltozós módszerek

Szemben azzal, amit sokan elsőre gondolnának, hogy ti. az egyváltozós módszerekkel egyetlen változót vizsgálunk (míg a többváltozósakkal többet), valójában egyváltozós módszerekkel is vizsgálhatunk akárhány változót. A különbség tehát nem ez, hanem az, hogy az egyváltozós módszerekkel egy időben egyetlen változót vizsgálunk csak, míg a többváltozós módszerek egyidejűleg is több változót tekintenek. (Ha megadjuk, hogy pontosan hányat, akkor ezt az elnevezésben is szerepeltethetjük, pl. kétváltozós vizsgálat, háromváltozós vizsgálat stb.)

Hogy mit értünk az alatt, hogy ,,egy időben’’? Képzeljünk el egy adatbázist, melyben emberek testmagasságát és testtömegét mértük le. Okkal várjuk azt, hogy a nagyobb testmagasság tendenciájában nagyobb testtömeggel jár együtt, tehát azoknak, akiknek nagyobb a testmagasságuk, várhatóan⁴ nagyobb a testtömegük is. Igen ám, de ha önmagában csak a testmagasságot vizsgáljuk, vagy csak a testtömeget, akkor ezt soha nem vennénk észre! Vegyük észre, hogy bármilyen alapos elemzést is végeznénk (beleértve akár az összes megfigyelés tömörítés nélküli felsorolását), soha nem jövünk rá erre a kapcsolatra – hiszen a külön-külön végzett vizsgálatokban nem tudjuk összerendelni az ugyanazon emberhez tartozó testmagasságot és testtömeget (épp ez a definíciója a külön-külön végzésnek). Amit tehát elvesztünk, az a változók közötti kapcsolatok kérdésköre. Éppen ezért mondhatjuk azt, hogy egy többváltozós vizsgálat több, mint több egyváltozós vizsgálat – hiszen itt már megjelenik a változók közötti kapcsolatok kérdése is.

Végezetül megjegyezzük, hogy a többváltozós kategóriát néha szétbontják, arra tekintettel, hogy a többváltozós elemzés klasszikus arzenálja csak egy-két tucat változóig alkalmazható hatásosan (sőt, igazán hatásosan inkább csak 10-nél is kevesebb változóra). Az e fölötti tartományban néha megkülönböztetésül sokváltozós adatelemzésről beszélnek.

3.2.3 A vizsgált változó(k) mérési skálája

A leíró statisztika módszerei jellegzetesen eltérnek aszerint is, hogy milyen mérési skálán mért változó elemzéséről van szó. Amint már említettük is, az ordinális és nominális változókat nem fogjuk megkülönböztetni, és egységesen minőségi változókról fogunk beszélni, hasonlóképp az intervallum- és arányskálán mért változók esetében is egységesen mennyiségi változókról lesz szó. (A különbségekre csak utalni fogunk.)

3.3 Minőségi változó egyváltozós elemzése

Minőségi változóra jó példa adatbázisunk rassz (race) változója, mely az alany rassz szerinti hovatartozását adja meg és ilyen módon nominális.

3.3.1 Analitikus eszközök

Ilyen változó elemzésének tipikus analitikus eszköze a gyakorisági sor. A gyakorisági sor a változó lehetséges kimeneteit (kategóriáit) tartalmazza, együtt azzal, hogy az adott kimenet hányszor fordult elő az adatbázisban. Az ilyen ,,darabszámot’’ a statisztikában általában is gyakoriságnak nevezik, és $f$-fel jelölik. (Illetve, ha utalni akarunk arra, hogy az $i$-edik kategória gyakoriságáról van szó, akkor $f_i$-vel.) Általában $n$-nel szokás jelölni a mintanagyságot, így $\sum_{i=1}^n f_i = n$.

Szokás még beszélni relatív gyakoriságról is, ami nem más, mint az előbbi (abszolút) gyakoriság osztva a mintanagysággal (azaz $n$-nel). A relatív gyakoriság tehát azt mutatja meg, hogy egy kategóriába a megfigyelési egységek mekkora hányada esik. Természetesen $\sum_{i=1}^n g_i = 1$.

Példának okáért, a rassz változó gyakorisági sora:

birthwt$race <- factor(birthwt$race, levels = 1:3,
                       labels = c("Kaukázusi", "Afroamerikai", "Egyéb"))
table(birthwt$race)

## 
##    Kaukázusi Afroamerikai        Egyéb 
##           96           26           67

prop.table(table(birthwt$race))

## 
##    Kaukázusi Afroamerikai        Egyéb 
##    0.5079365    0.1375661    0.3544974

cbind(table(birthwt$race), prop.table(table(birthwt$race)))

##              [,1]      [,2]
## Kaukázusi      96 0.5079365
## Afroamerikai   26 0.1375661
## Egyéb          67 0.3544974

Megjegyezzük, hogy a teljes relatív gyakorisági sort a statisztikusok nagyon gyakran a változó megoszlásának hívják.

Vegyük észre, hogy ebben a speciális esetben az információtömörítés igazából semmilyen információveszteséggel nem járt: ez a három szám pontosan ugyanúgy hordoz minden információt erről a változóról mint az eredeti 189 szám! Ez azonban egy abszolút speciális eset, ami kizárólag a változó minőségi mivoltának volt köszönhető.

A gyakorisági soron kívül egy mutatószámnak van még értelme ennél a mérési skálánál: a módusznak. A módusz (jele: $\mathrm{Mo}$) nem más, mint a leggyakoribb⁵ kimenet (tehát az a kimenet, melyhez tartozó gyakoriság a legnagyobb az adatbázisban). Nagyon formalizálva ezt írhatnánk: \[ \mathrm{Mo}=\mathop{\mathrm{arg\,max}}_i f_i. \]

A példánkban tehát a rassz módusza a kaukázusi.

Már most megjegyezzük, hogy a módusz ún. középérték, ezen belül is helyzeti középérték; de e fogalmaknak majd a mennyiségi változóknál lesz szemléletesebb tartalma.

Érdemes megfigyelni, hogy itt viszont már érvényesül a kompromisszum a hűség és az áttekinthetőség között! Nyilván még áttekinthetőbb, ha a fenti 3 szám megadása helyett annyit mondunk, hogy ,,a módusz a kaukázusi’’, de ebben már nagyon is lesz információveszteség: nem tudhatjuk, hogy a 189-ből 189 kaukázusi vagy 64 (vagy épp 96), és semmit nem tudunk a többi kategória gyakoriságáról.

Végezetül megjegyezzük, hogy az ordinalitás csak annyit módosít a fentieken, hogy a gyakorisági sorban a kategóriák felsorolási sorrendje kötött⁶ lesz (nominális esetben, mint amilyen a mostani példánk is volt, nyilván érdektelen, hogy milyen sorrendben adjuk meg a kategóriákat, tetszőlegesen felcserélhettük volna a sorokat anélkül, hogy az érdemi változást okozott volna).

Ami a mutatószámokat illeti, ordinális esetben elvileg már definiálható lenne a medián fogalma is, de mivel használata itt nem tipikus, a bevezetését meghagyjuk későbbre.

3.3.2 Grafikus eszközök

A minőségi változók grafikus elemzése lényegében a gyakorisági sor vizualizálását jelenti. Ennek két, gyakorlatban legtipikusabb eszköze az oszlopdiagram és a kördiagram. Az előbbi oszlopok magasságával, az utóbbi körcikkek területével szemlélteti a gyakoriságokat. (Bár ez utóbbi, jellegéből adódóan, igazából csak relatív gyakoriságokat tud szemléltetni. Oszlopdiagrammal gyakoriság és relatív gyakoriság is szemléltethető; sőt, a kettő lényegében ekvivalens, csak a függőleges tengely skálázása lesz más.)

Oszlopdiagramot használtunk @aref(fig:oszlopdiagram). ábrán.

barplot( table( birthwt$race ), xlab = "Rassz", ylab = "Gyakoriság [fő]" )

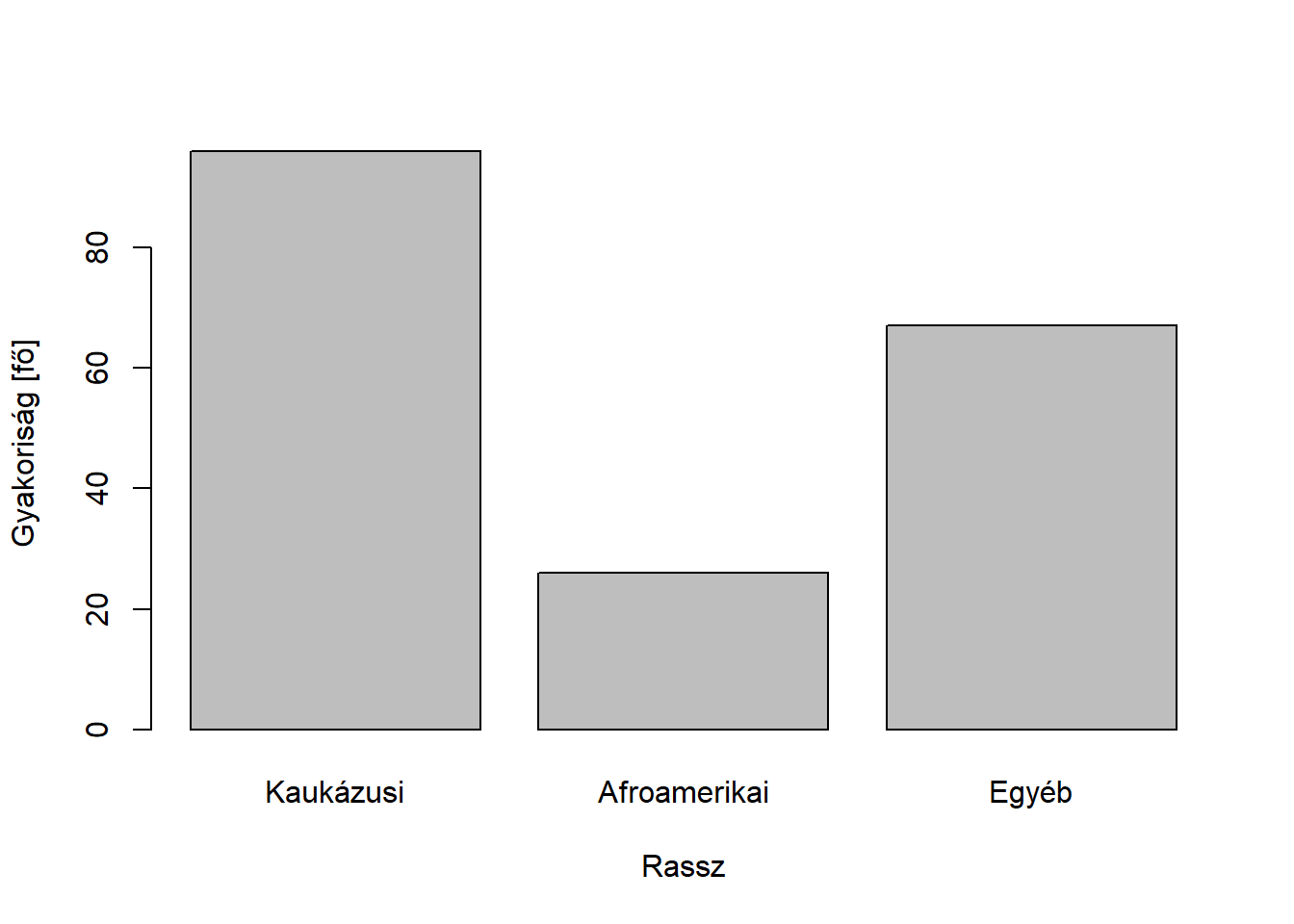
Ábra 3.1: Példa egy minőségi változó ábrázolására oszlopdiagrammal.

Az oszlop- és kördiagramok használata kapcsán megjegyzendő, hogy tudományos munkákban általában az oszlopdiagram a preferált, pszichológiai vizsgálatok szerint ugyanis az emberi szem jobban tud lineáris mértékeket kezelni és értelmezni, mint területet. Az egyetlen megfontolás, ami mégis az oszlopdiagram ellen szólhat néha, hogy az oszlopok kirajzolási sorrendje már implikál egyfajta sorrendezést (a természetes balról-jobbra olvasás miatt), ami adott esetben nem következik az változó tartalmából.

Az ordinalitás e téren nem sok változást okoz: az oszlopok sorrendje kötött lesz, illetve ábrázolhatóvá válik a kumulált gyakoriság is (természetesen csak oszlopdiagrammal).

3.4 Mennyiségi változó egyváltozós elemzése

Mennyiségi változóra jó példa adatbázisunk születési tömeg (bwt) változója, mely az alany születési tömegét adja meg (és így arányskálán mért, egész pontosan).

3.4.1 Analitikus eszközök

Az analitikus eszközök közül először most is a gyakorisági sort, majd a különböző mutatószámokat tárgyaljuk meg.

3.4.1.1 Gyakorisági sor

Gyakorisági sor természetesen mennyiségi változóra is készíthető, de csak módosításokkal. Annak ugyanis, hogy megszámoljuk, hogy az egyes előforduló kimenetekből mennyi van, nincs sok értelme (hogy egy példával illusztráljuk: az itt tipikus folytonos változóknál könnyen lehet, hogy minden egyes előforduló kimenetből csak egyetlen egy lesz). A problémát nyilván a folytonosság jelenti, ami ellen úgy védekezhetünk, hogy nem adott értéket felvev} megfigyelési egységek számát adjuk meg, hanem adott intervallumba esőek számát. Így kapjuk az osztályközös gyakorisági sort. (Az elnevezés arra utal, hogy osztályközöket hozunk létre – így fogjuk hívni az előbb említett intervallumokat.) A gyakoriság, relatív gyakoriság, kumulált gyakoriság és kumulált relatív gyakoriság⁷ értelmezése változatlan. A születési tömeg változó osztályközös gyakorisági sora (precízebben szólva: egy lehetséges osztályközös gyakorisági sora; hiszen ez már függeni fog az osztályközök megválasztásától is), a következő:

tab <- table( cut( birthwt$bwt, seq( 500, 5000, 500 ) ) )
cbind( Ci0 = seq( 500, 4500, 500 ), Ci1 = seq( 1000, 5000, 500 ), fi = tab, gi = prop.table( tab ) )

##                  Ci0  Ci1 fi          gi
## (500,1e+03]      500 1000  1 0.005291005
## (1e+03,1.5e+03] 1000 1500  4 0.021164021
## (1.5e+03,2e+03] 1500 2000 14 0.074074074
## (2e+03,2.5e+03] 2000 2500 40 0.211640212
## (2.5e+03,3e+03] 2500 3000 38 0.201058201
## (3e+03,3.5e+03] 3000 3500 45 0.238095238
## (3.5e+03,4e+03] 3500 4000 38 0.201058201
## (4e+03,4.5e+03] 4000 4500  7 0.037037037
## (4.5e+03,5e+03] 4500 5000  2 0.010582011

Itt $C_{i0}$ és $C_{i1}$ az $i$-edik osztályköz alsó és felső határát jelöli, rendre. (Az megállapodás kérdése, hogy a határon lévő megfigyelési egységeket, például egy pont 2000 grammos újszülöttet hová sorolunk, ennek természetesen csak a kerekítésből adódó diszkrétség miatt van egyáltalán jelentősége.)

Vegyük észre, hogy ez a megoldás lényegében azt jelenti, hogy a mennyiségi változónkat első lépésben ,,lefokozzuk’’ minőségi változóvá, és utána alkalmazzuk – mint teljesen közönséges minőségi változóra – a korábban megismert módszert.

Elöljáróban jegyezzük meg, hogy itt már a gyakorisági sor – szemben a minőségi esettel – igenis információvesztéssel jár: lehet 14 újszülött 1501 grammos, és lehet mind a 14 1999 grammos, mindkét esetben ugyanúgy a fenti osztályközös gyakorisági sort kapjuk. Az információvesztés mértékét nyilván az osztályközök hossza (a felosztás ,,finomsága’’) fogja meghatározni.

A sor előtti zárójeles megjegyzésünk már utal arra, hogy mi az osztályközös gyakorisági sorok használatának legnagyobb kihívása: az osztályközök helyes megválasztása. Az információveszteség minimalizálása szempontjából nyilván a minél szűkebb osztályközök a jobbak, viszont túlzásba ezt sem lehet vinni, különben értelmét veszti az egész eszköz, azáltal, hogy megszűnik a lényegkiemelő jelleg. (Ha egyre jobban és jobban szűkítjük az osztályközöket, akkor egy idő után visszajutunk oda, hogy az intervallumok túlnyomó részében 0 lesz a gyakoriság, a többiben pedig 1-1 – azaz lényegében visszakapjuk a minta ,,felsorolását’’.) Az egyetlen dolog, ami univerzálisan segít ezen, az a mintanagyság növelése (hiszen lehetővé teszi az osztályközök szűkítését úgy, hogy közben várhatóan nem csökken az egy osztályközbe eső megfigyelési egységek száma).

Ráadásul az osztópontok megválasztása nem csak az információveszteség szempontjából fontos. Az, hogy a gyakorisági sor milyen képest sugall számunkra a vizsgált változóról – sajnos – nagyban változhat akár az osztópontok nem túl lényeges áthelyezésének hatására is, különösen kis mintanagyságnál. Éppen ezért jelent a gyakorlatban komoly kihívást az osztályközök határainak jó megválasztása.

Hogy ezt hogyan tegyük meg, arra alapvetően két lehetőségünk van. Az egyik út az, hogy tárgyterületi információkat használunk fel, azaz megpróbálunk – az adott változó jelentését is figyelembe véve – szakmailag értelmes, tartalommal bíró osztópontokat találni. (A fenti gyakorisági sor példa erre, hiszen kerek, emberi szem számára kényelmesen értelmezhető osztópontokat vettünk fel.) A másik lehetőség, hogy tisztán statisztikai alapon (tehát a változó tárgyterületi jelentésének felhasználása nélkül) döntünk – vannak módszerek, melyek pusztán a megfigyelések statisztikai jellemzői (nagyság, szóródás stb.) alapján igyekeznek ,,kitalálni’’, hogy hová érdemes rakni az osztópontokat ahhoz, hogy a lehető leginformatívabb gyakorisági sort kapjuk. Példának okáért, az egyik ilyen ismert analitikus szabály a Sturges-szabály, ami azt javasolja, hogy $\left\lceil \log_2 n+1\right\rceil$ darab azonos szélességű osztályközt vegyünk fel a mintaminimum és -maximum között.

3.4.1.2 Mutatószámok

A mutatószámok a megfigyelések valamilyen jellemzőjét próbálják meg egy-egy számba tömörítve megragadni. A következőkben aszerint csoportosítva mutatjuk be őket, hogy mi ez a megragadott jellemző.

3.4.1.2.1 Középértékek (centrális tendencia)

Centrális tendencia alatt azt értjük, hogy mi az az érték, ami körül csoportosulnak a megfigyelések. Függően a konkrét mutatótól, olyanokra gondolhatunk ez alatt, mint ,,közepes’, ,,tipikus’ vagy ,,átlagos’’ érték. A legtöbb statisztikai alkalmazás szempontjából ez a legfontosabb jellemzője a változónak, ezért ha csak egyetlen számmal jellemezhetjük a változót, az tipikusan a centrális tendencia valamilyen leírója lesz. Ezeket a mutatószámokat általában középértéknek vagy helyzetmutatónak nevezik.

A centrális tendencia legismertebb mutatója a (számtani) átlag, jele $\overline{x}$. Definíciószerűen nem más, mint az az szám, amivel helyettesítve minden megfigyelési egység értékét, az ún. értékösszeg (a változó megfigyeléseinek összege) változatlan maradna: \[ \overline{x}=\frac{\sum_{i=1}^n x_i}{n}. \]

Azonnal látható, hogy ennek akkor van értelme, ha a különböző megfigyelések számtani összege valamilyen értelmes tartalommal bír. (Van például értelme beszélni egy osztály átlagos testtömegéről, hiszen a testtömegek összege értelmes kifejezés, megadja például, hogy mennyit mutatna egy mérleg, ha mindenki ráállná.) Ha azonban a változó olyan, hogy nem az megfigyelések összegének van értelme, akkor a számtani átlag használata félrevezető lehet, és mással kell helyettesíteni – például, ha a megfigyelések összege helyett azok szorzata a tárgyterületileg értelmes, akkor az ún. mértani átlaggal. (Tipikus példa erre az, ha a változó valamilyen növekedési ütemet jelent időben. Ha egy alany testtömege egy évben 1,2-szeresére nőtt, rákövetkező évben pedig 1,3-szeresére, akkor az össznövekedés nyilván nem a növekedések összege ($1,\!2 + 1,\!2 = 2,\!4$), hanem azok szorzata ($1,\!2 \cdot 1,\!2 = 1,\!44$) lesz.)

A születési tömegek átlaga 2944.5873016 gramm, ami azt jelenti, hogy az adatbázisban szereplő újszülöttek össz-testtömege akkor maradna változatlan, ha mindegyikük 2944.5873016 gramm lenne.

Az átlag ún. számított középérték, mivel valamilyen számszerű összefüggésben van a megfigyelések értékeivel.

Az átlag előnye, hogy rendkívül közismert, mindenki számára kényelmesen kezelhető, szokásos gondolkodásunkhoz közel álló mutató. (Ez olyannyira erős tényező, hogy nagyon sok orvosi publikáció még akkor is erőlteti az átlag használatát, amikor az – a mindjárt részletezendő okokból – nem célszerű.)

Az átlag legnagyobb hátránya, hogy nem robusztus. Egy statisztikai mutatószám robusztussága azt méri, hogy mennyire érzékeny arra, ha a mintában a többi értéktől, a csoportosulás alaptendenciájától jelentősen eltérő érték vagy értékek vannak. Az ilyen megfigyeléseket egyébként nagyon gyakran outliernek is nevezik. (,,Érzékenység’’ alatt azt értjük, hogy a mutatót mennyire tudja befolyásolni, eredeti értékétől eltéríteni ilyen outlierek jelenléte.) Az átlag ilyen szempontból extrém rossz mutató: egyrészt bármelyik megfigyelés bármilyen megváltozása módosítja az átlag értékét, de ami az igazán nagy baj, hogy ha egyetlen megfigyelés is tart a végtelenhez, úgy az átlag is tart a végtelenhez, függetlenül az összes többi megfigyeléstől, és függetlenül a minta nagyságától. Mindez azt mondja nekünk, hogy ha csak egyetlen outlier is van a mintában, már az is képes arra, hogy teljesen értelmetlenné tegye az átlagot. (Hiszen ha van egy ilyen outlier a mintában, akkor az átlag pont hogy nem a minta ,,közepes’’ értékét fogja mutatni, hanem egyre inkább az outlierét, minél jobban kilóg.)

Megjegyezzük, hogy pontosan emiatt az átlag használata a centrális tendencia jellemzésére nem csak gyakorlati szempontból lehet problémás (adatrögzítési hibákból, adatbázis-sérülésekből eredeti outlierek), hanem elméletileg is ellenjavallt, ha a változó olyan, hogy fel kell készülni kis számú, de a többitől lényegesen nagyobb vagy kisebb megfigyelés jelenlétére. (Ez fordulhat elő – mindenféle adatrögzítési és egyéb hiba nélkül is! – például ún. aszimmetrikus eloszlásoknál, melyekről később fogunk részletesebben beszélni.)

Épp ezen a robusztussági problémán igyekszik javítani a trimmelt (vagy nyesett) átlag: ezt úgy kapjuk, hogy elhagyjuk a legkisebb és legnagyobb adott számú elemet, és csak a maradékot átlagoljuk ki. Tipikusan az elhagyott megfigyelések száma alul és felül is a mintanagyság 2,5%-a; ebben az esetben 5%-os trimmelt átlagról beszélünk. (Bár elsőre ez szokatlan mutatónak tűnhet, és a tudományos irodalomban tényleg ritkábban is használják, de számos pontozásos sportágban épp ilyen elven alakítják ki a zsűri ,,átlagos’’ pontszámát.) A születési tömegek 5%-os trimmelt átlaga 2957.4152047 gramm, ami egyúttal azt is mutatja, lévén, hogy közel van a szokásos átlaghoz, hogy a születési tömegek aránylag szimmetrikus eloszlásúak, vélhetően komoly outlier nélkül.

Alapvetően más megközelítését jelenti a centrális tendencia megragadásának a medián használata, melynek jele $\mathrm{Me}_x$. A medián nem más, mint a nagyság szerint sorbarendezett megfigyelések közül a középső. (Amennyiben a mintanagyság páros, úgy nyilván két ,,középső’’ is van, ez esetben megállapodás kérdése, hogy mit nevezünk mediánnak; vehetjük például a kettő átlagát.) Úgy is szoktak fogalmazni, hogy a medián felezőpont, az az érték, amiről elmondható, hogy alatta és felette is egyaránt ugyanannyi mintaelem (az összes fele-fele) található.

Értelemszerű, hogy a medián szintén a centrális tendenciát jellemzi, csak épp kevésbé megszokott módon, mint az átlag – ez egyúttal használatának egyik fő gátja is: sok ember számára a medián tartalma (és egyáltalán, értelme) kevésbé ismert, így e mutató nem annyira jól kezelhető. Előnye viszont a robusztusság, ilyen szempontból az átlaggal szemben a másik végpontot képviseli: míg az átlag extrém érzékeny volt, addig a medián extrém robusztus. A minta minden medián feletti értéke (az egyszerűség kedvéért most gondoljunk páratlan mintanagyságra) tetszőlegesen megnövelhető (akár az összes egyszerre is), vagy a medián alatti értékek tetszőlegesen lecsökkenthetőek (akár az összes egyszerre is), vagy akár a kettő együtt is, a medián értéke nem változik! Hátránya, hogy a jó robusztusságért cserében kevesebb információt használ fel a mintából⁸; ezt épp a mintaértékek meglehetősen szabad ,,állítgathatósága’’ mutatja. (Hogy ez miért baj, az precízen csak induktív statisztikai keretben lehet megérteni, az ottani tárgyalás után már érthető lesz, hogy mit jelent az, hogy a medián kevésbé hatásos becslő mint az átlag.) A tanulság az, hogy ha feltehető, hogy a háttéreloszlás szimmetrikus-közeli, akkor érdemes átlagot használni, ha nem, vagy outlierek jelenlétére is fel kell készülni (azaz indokolt robusztus statisztika használata), akkor jobb a medián ilyen szempontból.

A születési tömegek mediánja 2977 gramm, azaz a 2977 gramm az a testtömeg, amiről elmondható, hogy az újszülöttek fele kisebb ennél, fele nagyobb.

Ahogy a medián a minta ,,felezőpontja’’ ugyanúgy definiálhatók általános osztópontok; ezeket kvantiliseknek nevezzük. A $p$-kvantilis ($0<p<1$) az az érték, amiről elmondható, hogy a megfigyelések $p$-ed része kisebb nála, $\left(1-p\right)$-ed része nagyobb nála. (Tehát a medián az $1/2$-kvantilis.) Gyakorlati szempontból nagyobb jelentősége van még a negyedelőpontoknak, melyek neve kvartilis. Ilyenből tehát nyilván három van: a $p=1/4,2/4=1/2,3/4$-kvantilis, ezek közül a középső persze ugyanaz mint a medián. A másik kettőt alsó és felső kvartilisnek szokták nevezni, és $Q_1$-gyel, illetve $Q_3$-mal jelölik. Tehát például $Q_1$ az a szám, amire igaz, hogy a minta egynegyede (darabszámra) nála kisebb értékű, háromnegyede nála nagyobb. Ezek valójában már nem is a centrális tendenciát, hanem általában az eloszlás alakját mutatják, mégpedig robusztus módon (ugyanazon okból, mint amit a mediánnál is láttunk). Ritkábban, de szokták használni ugyanerre a célra a tizedelőpontokat, nevük decilis ($D_1,D_2,\ldots,D_9$) és a századolópontokat, nevük percentilis ($P_1,P_2,\ldots,P_{99}$).

A módusz használatának a folytonosság miatt általában nincs értelme mennyiségi változó esetén, ahogy azt már említettük is. Értelmet csak az ad neki, ha diszkretizáljuk (csoportosítjuk) az adatokat, ahogy az a gyakorisági sorral történt is. Ilyenkor már van értelme móduszról beszélni, persze ekkor már csak osztályköz szintjén – szokás ezt modális osztályköznek is nevezni. Például a születési tömegek fent közölt osztályközös gyakorisági sorában (ne feledjük, itt már az is számít, hogy melyik osztályközös gyakorisági sorra vonatkozóan adjuk meg!) a modális osztályköz a 3000–3500 gramm.

A módusz és a medián ún. helyzeti középérték, mivel nem számítás eredményeként adódnak, hanem a többi megfigyeléshez képest elfoglalt helyzetük tünteti ki őket.

Ennek kapcsán azt is megjegyezzük, hogy átlagot, mediánt (és általában minden egyéb mutatószámot is) lehetséges osztályközös gyakorisági sorból (a nyers mintaelemek ismerete nélkül is) számolni, persze ekkor már csak közelítő jelleggel.

3.4.1.2.2 Szóródás

Szóródásnak nevezzük azt, hogy a megfigyelések milyen szorosan csoportosulnak azon érték körül, ami körül csoportosulnak (lásd a centrális tendenciát!), más szóval mennyire ingadoznak a megfigyelések, mekkora változékonyság van bennük. A gyakorlatban ez a második legfontosabb kérdés: ha csak egy jellemzőt adhatunk meg, akkor az a centrális tendencia lesz, de ha kettőt, akkor megadjuk azt is, hogy mekkora a szóródás.

A minta szóródásának legegyszerűbb mérőszáma a legkisebb ($\mathrm{Min}$) és a legnagyobb ($\mathrm{Max}$) mintaelem értéke, a mintaminimum és mintamaximum, illetve kettejük különbsége, melyet terjedelemnek nevezünk és $R$-rel jelölünk: $R=\mathrm{Max}-\mathrm{Min}$. Ezek előnye, hogy teljesen egyértelmű a tartalmuk, hátrányuk, hogy rendkívül érzékenyek arra, hogy konkrétan milyen mintát vettünk a sokaságból, ezért következtetési célokra nem is szokták alkalmazni.

A születési tömegek mintaminimuma 709 gramm, mintamaximuma 4990 gramm, így e változó terjedelme 4281gramm.

A leggyakoribb általános célú mutatója a szóródásnak a szórás, jele általában $s_x$ vagy $\sigma_x$. (A kettő neve nem keverendő: a ,,szóródás’’ a jellemző, a ,,szórás’’ egy lehetséges mutatószáma a szóródásnak.) A szórás nem más, mint a megfigyelések átlagtól vett átlagos eltérése. Ez utóbbi átlag alatt négyzetes átlagot értve – egyszerű számtani átlag nem lenne jó, hiszen azzal a pozitív és negatív irányú eltérések csökkentenék (sőt, belátható, hogy kioltanák) egymás hatását. Azaz: \[ s_x=\sqrt{\frac{\sum_{i=1}^n \left(x_i-\overline{x}\right)^2}{n}}. \]

Ennek a négyzetét szokás szórásnégyzetnek vagy varianciának nevezni. Deskriptív esetben néha inkább mintaszórást illetve mintavarianciát mondanak (hogy a megfelelő valószínűségszámítási fogalomtól megkülönböztessék).

A fent definiált mutatót szokás precízen korrigálatlan mintaszórásnak nevezni, ezzel szemben a korrigált mintaszórás: \[ s_x^{\ast}=\sqrt{\frac{\sum_{i=1}^n \left(x_i-\overline{x}\right)^2}{n-1}}. \] A különbségük oka csak a következtető statisztikában válik világossá (a korrigálatlan mintavariancia, első ránézésre talán meglepő módon, nem torzítatlan becslője a sokasági varianciának).

A születési tömegek korrigált mintaszórása 729.2142952 gramm, tehát az újszülöttek testtömegeinek átlaguk körül vett ingadozásának (négyzetes) átlaga 729.2142952 gramm.

A szórás hátránya, hogy – az átlaghoz hasonlóan – nem robusztus mutató. (Egyrészt azért, mert maga is az eltérések négyzetét használja, ami érzékeny a kilógó értékekre, másrészt azért, mert a eltéréseket a nem-robusztus átlagtól veszi.) Egyik lehetséges megoldás az interkvartilis terjedelem (jele $IQR$) használata, ami a felső és az alsó kvartilis különbsége: \[ IQR=Q_3-Q_1. \] Az interkvartilis terjedelem a robusztus kvartiliseken alapul, így robusztus mutató, és könnyen látható, hogy tartalmilag a szóródást jellemzi, hiszen minél jobban szóródott az eloszlás, annál távolabb lesz az alsó és a felső negyedelőpontja.

A születési tömegek interkvartilis terjedelme 1073 gramm, tehát az a tömeg, ami fölött az újszülöttek egynegyede (és alatta háromnegyede) van, 1073 grammal nagyobb annál a tömegnél, ami fölött az újszülöttek háromnegyede (és alatta egynegyede) van.

A másik lehetőség a szórás ,,megjavítása’, olyan módon, hogy az eltéréseknek nem a négyzetét, hanem az abszolút értékét vesszük. (Ezzel a kapott mennyiség matematikai kezelhetőségét rontjuk, hiszen a négyzetreemelés jobban kezelhető matematikai objektum, de a robusztusságot növeljük.) További javítási lehetőség, ha az eltéréseket nem az átlagtól hanem a mediántól vesszük, és nem is átlagoljuk őket, hanem a mediánjukat képezzük. A mutató neve, ami mindhárom ,,trükköt’ beveti: medián abszolút eltérés, jele $MAD$, tehát \[ MAD=\mathrm{Me}\left(\left|x_i-\mathrm{Me}\left(x\right)\right|\right). \] (A szakirodalom itt nem teljesen egyértelmű: néha $MAD$-nak nevezik azt a mutatót is, ahol csak az első javítást csinálják meg, tehát abszolútértéket vesznek, de azokat továbbra is csak átlagolják, és az eltéréseket is az átlagtól veszik.)

A születési tömegek medián abszolút eltérése 563 gramm, tehát az újszülöttek testtömegeinek mediánjuk körül vett (abszolút) ingadozásának mediánja 563 gramm.

3.4.1.2.3 Alakmutatók

A fenti két jellemzőn túlmenően néha egyéb, még inkább részletekbe menő jellemzőit is használják egy változó leírásának. Egy tipikus példa erre a szimmetria: egy eloszlás szimmetrikus, ha a centrális tendencia helyétől mindkét irányban nagyjából hasonló a lefutása. (Vegyük észre, hogy ez nem következik még abból sem, ha két változóra ugyanaz a centrális tendencia, és ugyanaz a szóródás: ettől még az egyik lehet szimmetrikus, míg a másik nem.) A nem szimmetrikus eloszlásokat szokás ferde eloszlásoknak is nevezni; ezen belül is szoktak balra ferde (jobbra hosszan elnyúló) és jobbra ferde (balra hosszan elnyúló) eloszlásról beszélni, attól függően, hogy melyik irányban nagyobb a szóródás. További kérdések is felmerülnek, mint a csúcsosság, a multimodalitás stb. – ezekkel és a továbbiakkal azonban részletesen itt nem foglalkozunk.

3.4.2 Grafikus eszközök

A grafikus eszközök közül először a hisztogramot, utána röviden a magfüggvényes sűrűségbecslőt, majd végül a boxplotot tárgyaljuk meg.

3.4.2.1 Hisztogram

A hisztogram leegyszerűsítve nem más, mint az osztályközös gyakorisági sor ábrázolása oszlopdiagramon, annyi specialitással, hogy az oszlopokat közvetlenül egymás mellé rajzoljuk, hely kihagyása nélkül (3.2. ábra).

hist( birthwt$bwt, xlab = "Születési tömeg [g]", ylab = "Gyakoriság [fő]", main = "" )
rug( birthwt$bwt )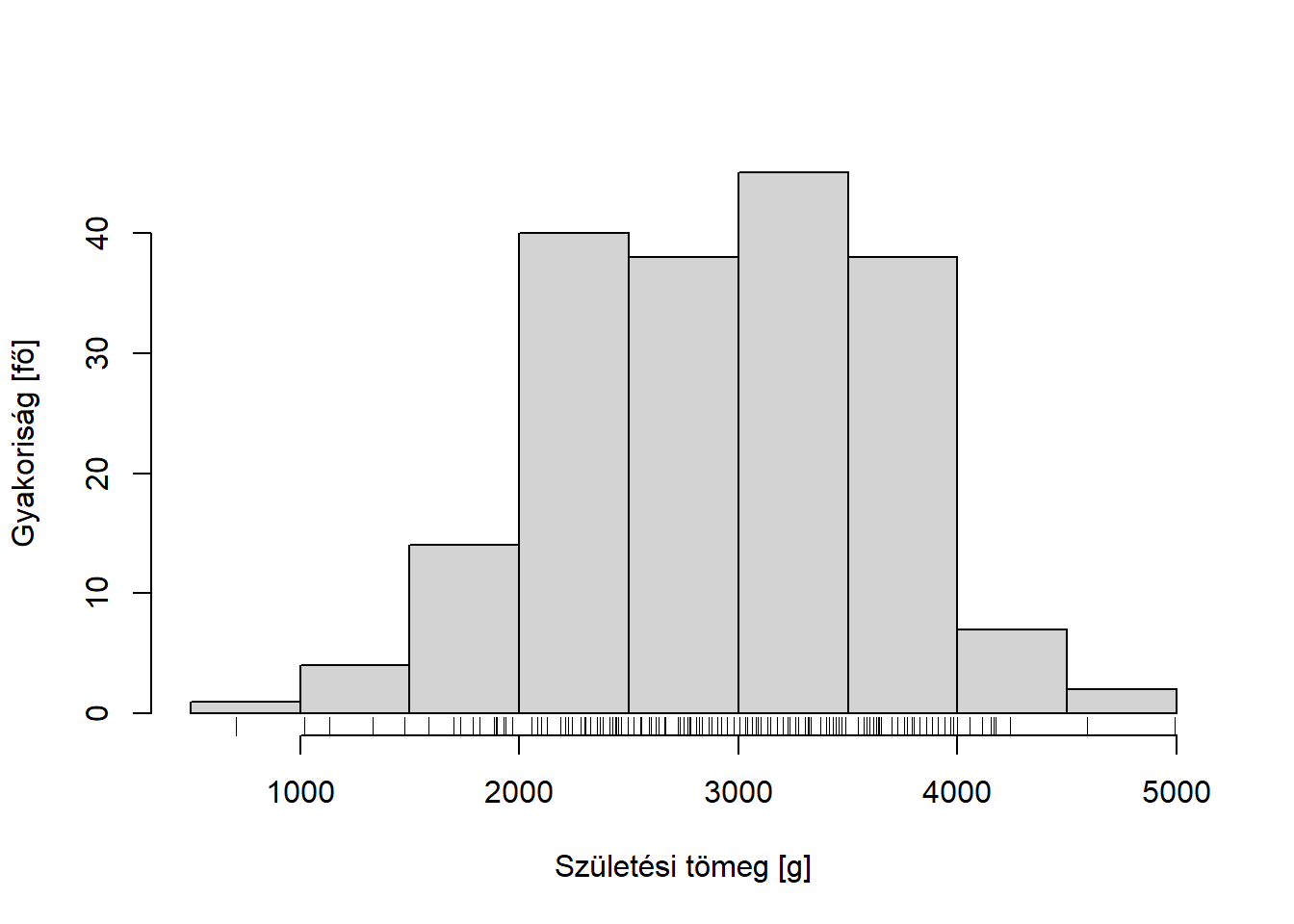

Ábra 3.2: Példa egy mennyiségi változó ábrázolására hisztogrammal.

Az ábrán látható, hogy az oszlopok határai kijelölik az osztályközöket (ezek természetesen nem feltétlenül azonos szélességűek); adott osztályköz fölé pedig \[ \frac{f_i}{n \cdot h_i} \] magasságú oszlopokat rajzolunk, ahol $h_i$ az adott osztályköz szélessége. Ezen az ábrán feltüntettük (alul, apró tüskékként) magukat a nyers megfigyeléseket is (,,rugplot’’).

A hisztogram a legnépszerűbb adatvizualizációs módszer mennyiségi változókra. Ahogy már utaltunk is rá, hatalmas előnye, hogy a vizuálisan közölt információ rendkívül jól feldolgozható az emberi agy számára: a fenti hisztogram alapján szinte ,,ránézésre’’, egyetlen pillantással jó képünk alakul ki a centrális tendenciáról, a szóródásról, sőt, az eloszlás alakjának finomabb jellemzőiről is. Egy átlagot még el sem olvastunk, amikorra a hisztogram alapján már olyan finom jellemzőkről, mint az eloszlás szimmetriája is képünk van.

Hátránya, hogy kevésbé objektív (mint a grafikus módszerek általában) – ha például két változót össze kell hasonlítanunk, akkor két átlaggal (azaz két számmal) az értelemszerűen könnyebben megtehető mint két hisztogrammal.

A legnagyobb kihívás azonban az osztályközök helyes megválasztása. Ez a probléma teljesen ugyanaz, mint amit az osztályközös gyakorisági sornál is kifejtettünk. Sőt, itt talán még jobban szemléltethető: @aref(fig:hisztogramvalasztasok). ábrán ugyanazt az adatsort ábrázoltuk, csak épp az optimálisnál lényegesen több, illetve lényegesen kevesebb osztályközt használva is.

par( mfrow = c( 1, 3 ) )
hist( birthwt$bwt, 3, xlab = "Születési tömeg [g]", ylab = "Gyakoriság", main = "" )
hist( birthwt$bwt, xlab = "Születési tömeg [g]", ylab = "Gyakoriság", main = "" )
hist( birthwt$bwt, 30, xlab = "Születési tömeg [g]", ylab = "Gyakoriság", main = "" )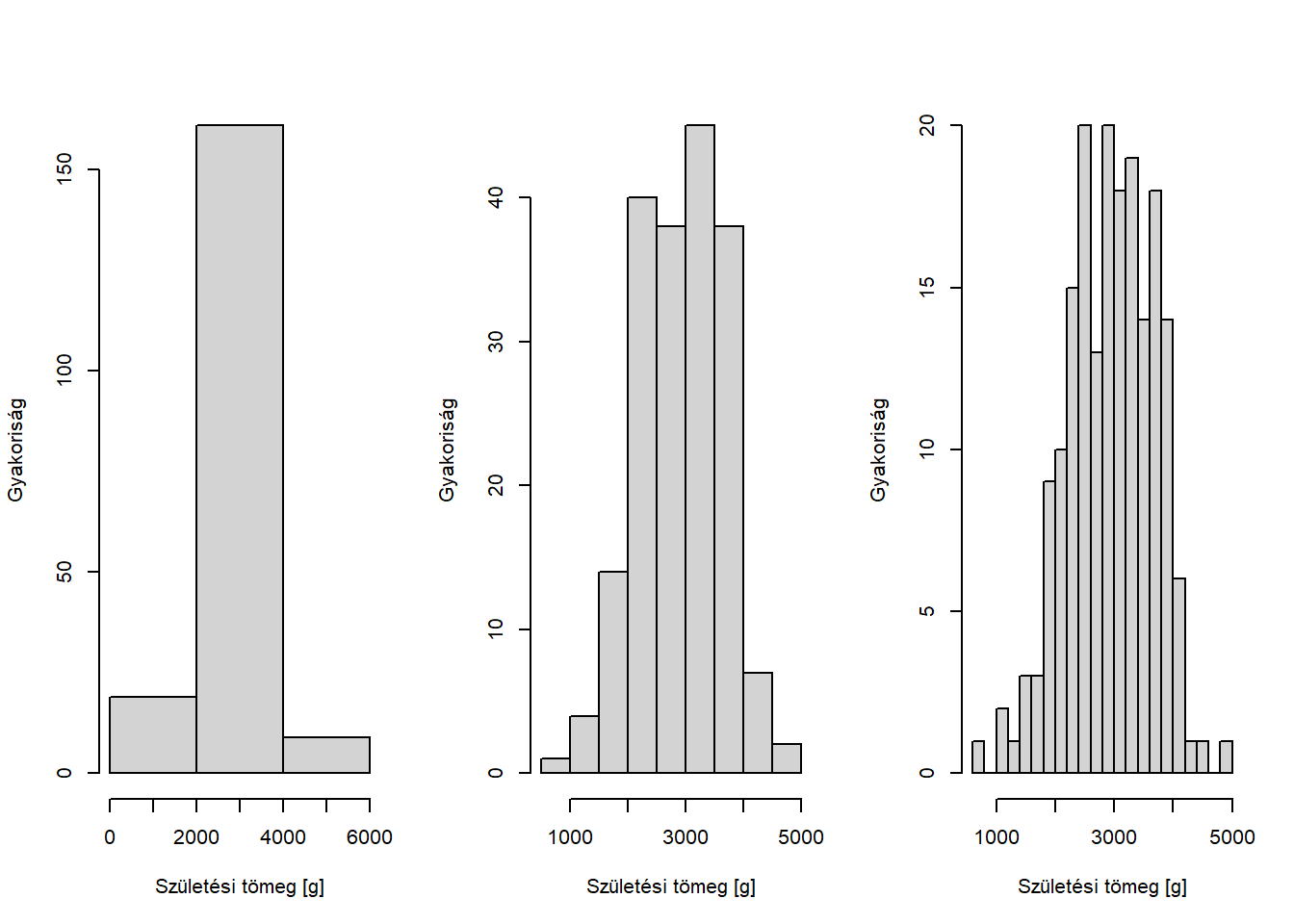

Ábra 3.3: Ugyanazon adatsor ábrázolása különféle számú osztályközt tartalmazó hisztogrammal.

Itt érzékelhető igazán, hogy miért probléma az is, ha túl finom, és az is, ha túl durva felosztást választunk (adott, rögzített mintanagyság mellett!). Amennyiben az osztályközök száma túl kevés, akkor sok információt vesztünk: az eloszlásról kapott kép összemossa a finomabb részleteket (bal oldal). Úgy is szokták mondani: nagy lesz a torzítás. Ha viszont túl sok osztályközt választunk, akkor rendkívül esetlegessé válik, hogy egy osztályközbe hány mintaelem esik, nagyon ingadozó lesz a magasság (jobb oldal), úgy szokták mondani: nagy lesz a variancia. (Ez itt a sok más helyen is megjelenő torzítás-variancia trade-off egy példája.) Ahogy sokszor elmondtuk: valamiféle optimumot kell találni a kettő között. Ennek módszereiről az osztályközös gyakorisági sornál már írtunk.

Az osztályközöket többféleképp is megadhatjuk R-ben:

Explicite megadjuk az osztályközök határait: hist( birthwt$bwt, breaks = c( 500, 1500, 2000, 2500, 2750, 3000, 3250, 3500, 5000 ) ).
Megadjuk az osztályközök számát: hist( birthwt$bwt, breaks = 10 ).
Megadjuk a szabály nevét, amivel kérjük az osztályközök számának kiszámolását: hist( birthwt$bwt, breaks = "Sturges" ).
Saját függvényt adunk meg, mely vagy az osztályközök számát, vagy a határait kiszámolja az adatok alapján.

3.4.2.2 Magfüggvényes sűrűségbecslő

A hisztogrammal kapcsolatos egyik probléma az előbb említett érzékenység az osztályközök megválasztására. Emellett felvethető az is, hogy a hisztogram szakaszonként konstans becslést ad, ami zavaró lehet (különösen, ha kicsi a mintanagyság, és emiatt nem tudunk sok osztályközt felvenni). Ez utóbbit kiküszöböli, és sok gyakorlati esetben az előbbit is enyhíti a magfüggvényes sűrűségbecslő alkalmazása. Ennek matematikai részleteivel most nem foglalkozunk, megelégszünk annyival, hogy a hisztogramhoz hasonlóan az eloszlás alakját becsli, ám a hisztogramtól eltérően nem szakaszonként konstans görbével (3.4. ábra).

plot( density( birthwt$bwt ), xlab = "Születési tömeg [g]", ylab = "Sűrűség", main = "" )

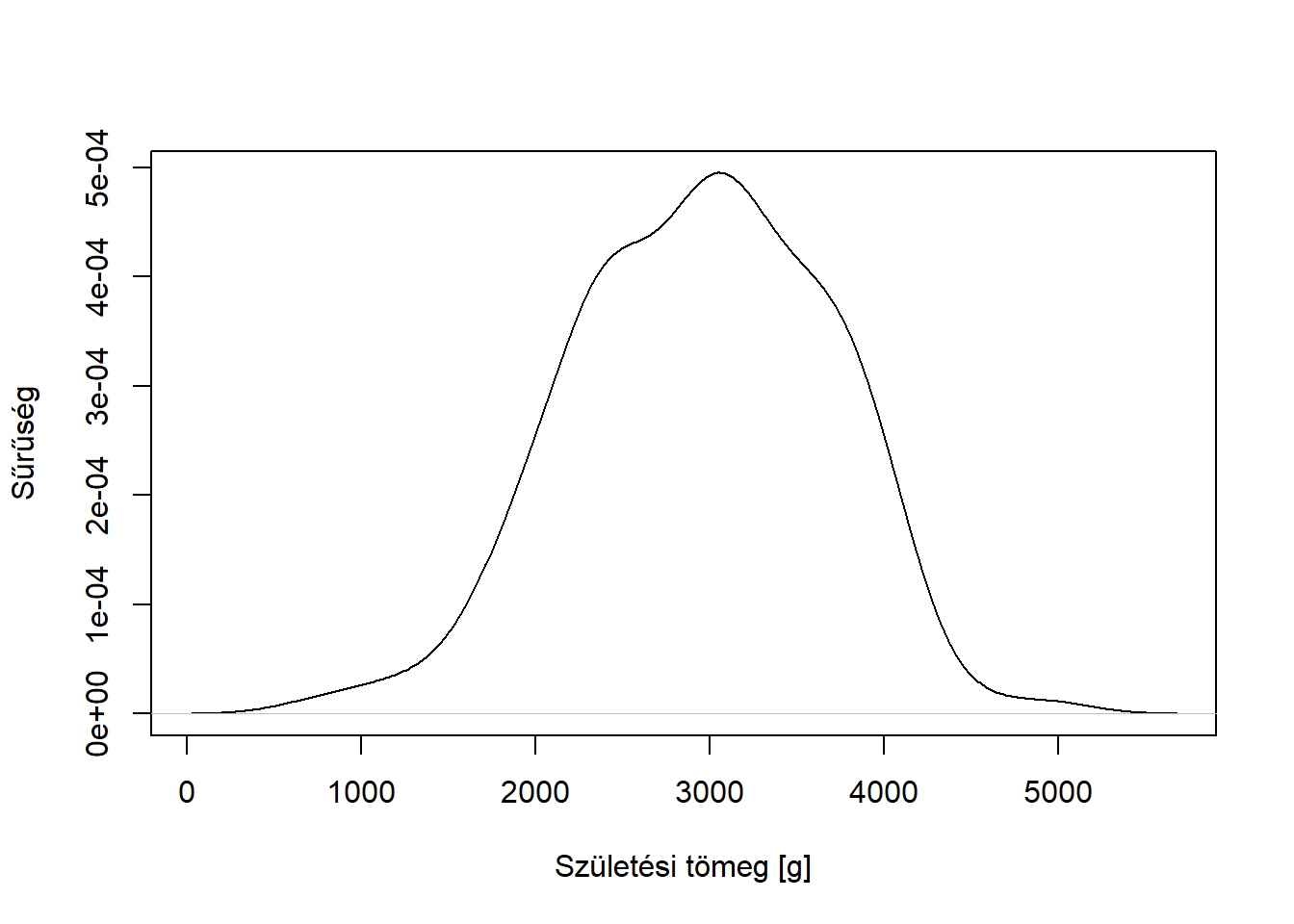
Ábra 3.4: Példa egy mennyiségi változó ábrázolására magfüggvényes sűrűségbecslővel.

Sajnos az osztályközök megválasztásának problémája teljesen nem oldódik meg, a magfüggvényes sűrűségbecslőnek is van ugyanis állítható paramétere (magfüggvény, és különösen az ún. sávszélesség). Ennek optimális megválasztása szintén probléma lehet, különösen, ha nagyon egyenetlen a mintaelemek eloszlása.

3.4.2.3 (Tukey-féle) boxplot

Végül egy egész más elven felépülő, de szellemes, és a gyakorlatban is nagyon hasznos vizualizációs módszerrel ismerkedünk meg, a (Tukey-féle) boxplottal (vagy ritkán használt magyar nevén: dobozábrával).

A boxplot nem más, mint egy számegyenes fölé rajzolt téglalap, mely egy adott változót reprezentál úgy, hogy a téglalap alsó széle az alsó kvartilisnél ($Q_1$-nél), a felső széle pedig a felső kvartilisnél ($Q_3$-nál) van. A téglalapon belül egy vastagabb függőleges vonal is látható, ez a mediánnál található (3.5. ábra).

boxplot( birthwt$bwt )

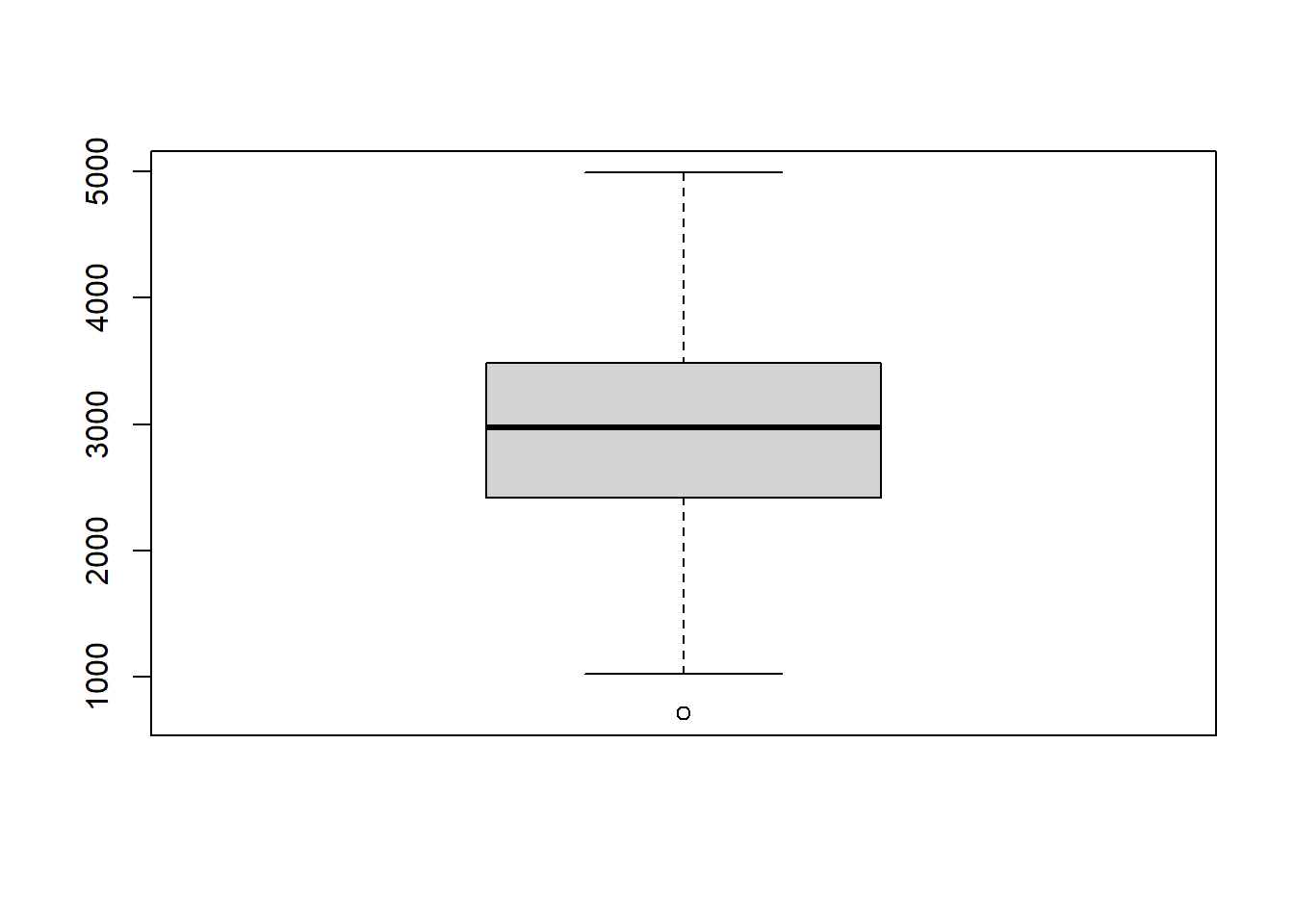
Ábra 3.5: Példa egy mennyiségi változó ábrázolására boxplottal.

A boxplotból két ,,antenna’’ nyúlik ki felfelé és lefelé. A boxplot alapváltozatában ezek a mintaminimumig és mintamaximumig nyúlnak ki, de a némileg haladóbb megvalósításban (amit a fenti ábra is mutat) az alsó antenna nem a minimumig terjed, hanem a legkisebb elemig, ami nem kisebb, mint $\mathrm{Me}-\alpha \cdot IQR$; hasonlóképp a felső antenna nem a maximumig terjed, hanem a legnagyobb elemig, ami nem nagyobb mint $\mathrm{Me}+\alpha \cdot IQR$. ($\alpha$ egy előre megadott konstans, tipikusan $\alpha=1,\!5$.) Azokat az elemeket melyek ezen kívül helyezkednek el, külön szimbólum, például kis karika jelöli. E mögött az a megfontolás, hogy így a boxplot egyszerű outlier-szűrést is lehetővé tesz: azok az elemek minősülnek outliernek, melyek az antennákon kívül helyezkednek el.

A boxplot jóval nagyobb információtömörítést hajt végre mint akár a hisztogram, akár a magfüggvényes becslő – ez részint hátránya, bár ennek ellenére gyakorlott szem számára így is meglehetősen jó információt hordoz az eloszlás alakjáról. Azonban ugyanez előnye is, hiszen kompakt (ami különösen jól jön akkor, ha például több csoportot kell összehasonlítani), valamint további nagy előnye, hogy – szemben mind a hisztogrammal, mind a magfüggvényes becslővel – semmilyen paraméter hangolását nem igényli, így kinézete teljesen egyértelműen meghatározott.

3.5 Minőségi változók kétváltozós elemzése

Minőségi változók kapcsolatát asszociációnak szokás nevezni a statisztikában. Erre jó példa adatbázisunk rassz (race) és irritábilis méh (ui) változói, mely az alany rassz szerinti hovatartozását és az irritábilis méh szindróma fennállását adja meg.

3.5.1 Analitikus eszközök

Ahogy már megbeszéltük, a kétváltozós vizsgálatok sava-borsa az lesz, hogy a változók kapcsolatáról is képesek leszünk nyilatkozni. Ahhoz, hogy precízen definiáljuk, hogy mit értünk kapcsolat alatt, elsőként bemutatjuk az kontingenciatáblát (vagy kombinációs táblát vagy kereszttáblát), mely egyúttal az egyik legfontosabb analitikus eszköz is lesz két minőségi változó kapcsolatának vizsgálatában. Ezt követően nagyon röviden beszélünk a kapcsolat jellemzésére használható mutatószámokról is.

3.5.1.1 Kontingenciatábla

A kontingenciatábla egy olyan táblázat, melynek soraiban és oszlopaiban a két változó lehetséges kimenetelei vannak, az egyes cellákban pedig azon megfigyelési egységek darabszáma (tehát gyakorisága), melyek a cella sora és oszlopa szerinti kimenetűek a sorhoz illetve az oszlophoz rendelt változó szerint. Például, a rassz és az irritábilis méh kontingenciatáblája így néz ki:

table( birthwt$race, birthwt$ui )

##               
##                 0  1
##   Kaukázusi    83 13
##   Afroamerikai 23  3
##   Egyéb        55 12

Tehát például 83 olyan megfigyelési egység van az adatbázisban, ahol az anya rassza kaukázusi és nincs irritábilis méh szindrómája 12 egyéb rasszú, és irritábilis méh szindrómában szenvedő alany van, és így tovább.

A kontingenciatábla szigorúan véve csak a $3 \times 2$ darab gyakoriságot jelenti; de néha összegző sorokat vagy oszlopokat írunk mellé:

tab <- table( birthwt$race, birthwt$ui )
rbind( cbind( tab, margin.table( tab, 1 ) ), cbind( t( margin.table( tab, 2 ) ), margin.table( tab ) ) )

##                0  1    
## Kaukázusi     83 13  96
## Afroamerikai  23  3  26
## Egyéb         55 12  67
##              161 28 189

Ezek neve: perem- vagy vetületi gyakoriság. (Mindkét elnevezés logikus: perem, hiszen a kontingenciatábla peremére kell ezeket ráírni, és vetületi, hiszen úgy kaphatjuk, hogy a kontingenciatáblát levetítjük vízszintesen vagy függőlegesen ,,levetítjük’, vetítés alatt most azt értve, hogy az egymásra ,,vetülő’ elemeket összeadjuk.) A 189 a mintanagyság.

A fenti gyakoriságokon túl természetesen relatív gyakoriságokról is beszélhetünk. A relatív gyakoriság definícióját közvetlenül alkalmazva kapjuk azt a lehetőséget, hogy mindegyik cellát leosztjuk a mintanagysággal, például a bal felső $83/189=43,\!9$% lesz. Ez az irritábilis méh szindrómában szenvedő kaukázusiak aránya a teljes mintán belül. A relatív gyakoriságokkal kitöltött kontingenciatábla peremei a relatív peremgyakoriságok (vagy relatív vetületi gyakoriságok). Szokás ezt peremmegoszlásnak vagy vetületi megoszlásnak is nevezni. (Az elnevezés nem meglepő: már korábban is utaltunk rá, hogy egy teljes relatív gyakorisági sort a statisztikusok általában megoszlásnak neveznek.)

Kontingenciatábla esetén azonban van egy másik – logikus – mód arra, hogy relatív gyakoriságot értelmezzünk: a 43,9% megadja, hogy az összes alany mekkora hányada kaukázusi és irritábilis méh szindrómában nem szenvedő, de minket érdekelhet az is, hogy az (összes helyett) csak az irritábilis méh szindrómában nem szenvedők mekkora hányada kaukázusi. Azaz: a 83-at nem a 189-cel, hanem a 161-gyel osztjuk le: $83/161=51,\!6$%. Ezt nevezzük feltételes relatív gyakoriságnak. Azért feltételes, mert ez egy relatív gyakoriság azon feltétel mellett, hogy valaki nem szenved irritábilis méh szindrómában. Más szóval: ha feltesszük, hogy az alanyaink nem szenvednek irritábilis méh szindrómában akkor közöttük 51,6% a kaukázusiak aránya. Ez természetesen kiszámolható a rassz változó másik két kimenetére is; az így kapott 51,6%–14,3%–34,2% egy teljes (csak épp feltételes) relatív gyakorisági sor, összege nyilván 100%. Szokás ezt a sorváltozó (esetünkben a rassz) feltételes megoszlásának is nevezni, az a oszlopváltozó (esetünkben az irritábilis méh) adott értéke (esetünkben: igen) mint feltétel mellett. Természetesen ugyanezek kiszámolhatóak a jobb oldali oszlopra is, ez magyarul azt jelenti, hogy az irritábilis méh nem kimenetére feltételezünk. Az eljárás ugyanez, azzal a különbséggel, hogy a jobb oldali számokat nyilván 28-cal kell leosztani. A feltételes relatív gyakoriság tehát nem más, mint a gyakoriság adott peremgyakorisággal osztva.

Természetesen nem csak az oszlopváltozóra feltételezhetünk! Pontosan ugyanígy van értelme beszélni az oszlopváltozó feltételes eloszlásáról a sorváltozó adott értéke, mint feltétel mellett. Például kijelenthetjük, hogy annak feltételes relatív gyakorisága, hogy egy alany nem szenved irritábilis méh szindrómában $83/96=86,\!5$% azon feltétel mellett, hogy kaukázusi a rassza. Hasonlóan továbbmenve azt is mondhatjuk, hogy az irritábilis méh fennállásának feltételes megoszlása azon feltétel mellett, hogy az alany kaukázusi, 86,5%–13,5%.

Összefoglalva, egy cellához négyféle számot is rendelhetünk, a bal felső példáján: 83 (gyakoriság), 43,9% (relatív gyakoriság), 51,6% (feltételes relatív gyakoriság azon feltétel mellett, hogy nem áll fenn irritábilis méh szindróma) és 86,5% (feltételes relatív gyakoriság azon feltétel mellett, hogy a rassz kaukázusi). Mindezeket szemléltetik a következő táblázatok.

Relatív gyakoriságok (peremeken a vetületi megoszlásokkal):

tab <- prop.table( table( birthwt$race, birthwt$ui ) )
rbind( cbind( tab, margin.table( tab, 1 ) ), cbind( t( margin.table( tab, 2 ) ), margin.table( tab ) ) )

##                      0          1          
## Kaukázusi    0.4391534 0.06878307 0.5079365
## Afroamerikai 0.1216931 0.01587302 0.1375661
## Egyéb        0.2910053 0.06349206 0.3544974
##              0.8518519 0.14814815 1.0000000

Irritábilis méh feltételes relatív gyakoriságai a rassz különböző kimenetei, mint feltétel esetén

tab <- prop.table( table( birthwt$race, birthwt$ui ), 1 )
rbind( cbind( tab, margin.table( tab, 1 ) ) )

##                      0         1  
## Kaukázusi    0.8645833 0.1354167 1
## Afroamerikai 0.8846154 0.1153846 1
## Egyéb        0.8208955 0.1791045 1

Rassz feltételes relatív gyakoriságai az irritábilis méh különböző kimenetei, mint feltétel esetén:

tab <- prop.table( table( birthwt$race, birthwt$ui ), 2 )
rbind( tab, t( margin.table( tab, 2 ) ) )

##                      0         1
## Kaukázusi    0.5155280 0.4642857
## Afroamerikai 0.1428571 0.1071429
## Egyéb        0.3416149 0.4285714
##              1.0000000 1.0000000

Természetesen nem arról van szó, hogy bármelyik jobb lenne, mint a többi – egyszerűen más elemzési célra alkalmasak. A feltételes megoszlásokra gondolva, az is érdekes kérdés lehet, hogy a kaukázusiak mekkora hányada szenved irritábilis méh szindrómában, és az is érdekes (de más tartalmú) kérdés, hogy az irritábilis méh szindrómában szenvedők mekkora hányada kaukázusi rasszú. Mindezek között egyszerű algebrai összefüggések állnak fenn, ezeket most nem részletezzük⁹.

Továbbhaladva, tökéletesen látható, hogy miért mondtuk, hogy a többváltozós elemzés az egyváltozós elemzések kiterjesztése: a fenti kétdimenziós kontingenciatáblában minden információ benne van, amit a két változót külön-külön elemezve látnánk: egyszerűen levetítjük a kontingenciatáblát a megfelelő dimenziós mentén és kapott vetületi gyakoriságok nem mások lesznek, mint a vetítési irány változójának gyakorisági sora! (Amiben minden információ benne van.)

Az tehát egyértelmű, hogy ez tartalmazza mindazt az információt, amit a két változó külön-külön végzett vizsgálata – csakhogy mi azt állítottuk, hogy többet is. Ez vezet el a változók kapcsolatának kérdéséhez. Minőségi változók esetében (kontingenciatáblán) akkor mondjuk, hogy két változó kapcsolatban van egymással, ha a sorváltozó feltételes megoszlásai ugyanazok, az oszlopváltozó bármely értékére is feltételezünk. Vagy – ami ezzel egyenértékű –: az oszlopváltozó feltételes megoszlásai ugyanazok, a sorváltozó bármely értékére is feltételezünk. (Ez első ránézésre, kicsit nagyvonalú volt, de belátható matematikailag, hogy a kettő valóban egyenértékű: ha az oszlopváltozó feltételes megoszlásai ugyanazok minden sorban, akkor a sorváltozó feltételes megoszlásai is ugyanazok minden oszlopban, és fordítva is, ha az oszlopváltozó feltételes megoszlásai nem ugyanazok minden sorban, akkor a sorváltozó feltételes megoszlásai sem ugyanazok minden oszlopban.)

Ez a definíció jogos: általánosságban véve is, az, hogy két változó között nincs kapcsolat, azt jelenti statisztikai nyelven, hogy az egyikre vonatkozó információból nem nyerünk információt a másikra vonatkozóan. Így már érthető ez a kontingenciatáblákra alkalmazott definíció: ha nincs kapcsolat, akkor hiába mondjak meg valaki, hogy mi – például – a sorváltozó értéke, ebből semmit nem tudunk meg az oszlopváltozó feltételes megoszlásáról (hiszen az minden sorban ugyanaz!). Ha van kapcsolat, akkor nyerünk plusz-információt (hiszen más lesz a feltételes megoszlása).

Látható, hogy ebben az esetben csak nagyon gyenge kapcsolatról beszélhetünk: a sorváltozó feltételes megoszlása mindkét oszlopban (precízen: az oszlopváltozó mindkét kimenetére feltételezve) nagyjából ugyanaz (kb. 50%–kb. 10%–kb. 40%), és az oszlopváltozó feltételes megoszlása is nagyjából ugyanaz mindhárom sorban (kb. 85%–kb. 15%). Ahogy már elmondtuk, az előbbi mondat bármelyik feléből automatikusan következik a másik fele. Itt tehát szemléletesen is látható a kapcsolat hiányának tartalma: hiába is mondja meg valaki, hogy az alany rassza kaukázusi, afroamerikai vagy egyéb, szinte ugyanúgy csak azt tudjuk mondani, hogy ,,akkor 85%–15% a megoszlás az irritábilis méh fennállása szerint’’. A rasszra vonatkozó információ nem adott szinte semmilyen információt a másik változóról.

Képzeljünk el ezzel szemben – másik végletként – egy olyan esetet, melyben a 189 alany közül 100 kaukázusi irritábilis méh szindróma nélkül, és 89 egyéb rasszú irritábilis méh szindrómával! Ebben az esetben az egyik változóra vonatkozó információ nem egyszerűen ,,elárul valamit’’ a másik változóról, hanem egyenesen determinálja azt: ha valaki elárulja, hogy egy alany kaukázusi rasszú, akkor biztosan tudjuk, hogy nem szenved irritábilis bél szindrómában, ha pedig azt mondja, hogy egyéb rasszú, akkor rögtön tudjuk, hogy szenved ebben. (Természetesen itt is igaz, hogy a dolog fordítva is működik: ha tudjuk, hogy egy alany nem szenved irritábilis méh szindrómában, akkor azonnal tudjuk, hogy kaukázusi, ha pedig nem szenved ebben, akkor biztos, hogy egyéb rasszú.) Ez a kapcsolat másik végpontja.

Zárásként megjegyezzük, hogy a statisztikában valójában nem így szokták bevezetni a kapcsolat fogalmát, hanem úgy, mint azt az esetet, amikor a két változó nem független egymástól; függetlenség alatt pedig azt értik, hogy az együttes megoszlás a vetületi megoszlások szorzataként áll elő. Érdemes végiggondolni, hogy ez valóban egybeesik a hétköznapi ,,függetlenség’’ fogalommal. Szintén érdemes végiggondolni, hogy ebből valóban következik a fenti definíció, de ezzel részletesebben nem foglalkozunk most.

3.5.1.2 Mutatószámok

A kapcsolat erősségének kvalitatív fogalmát fent megadtuk; erre több mutatót is definiáltak, melyekkel az erősség számszerűen is lemérhető. Amennyiben a változók nominálisak, úgy pusztán erre van lehetőség.

Ha azonban a változók ordinálisak, úgy értelmet nyert a kapcsolat irányának fogalma is. Ordinális változók esetén ugyanis a sorok és oszlopok sorrendje nem tetszőleges, van értelme mindkét változó szerint ,,nagyobb’’ és ,,kisebb’’ kimenetről beszélni. Innentől kezdve tehát nem csak azt mondhatjuk, hogy van kapcsolat, ha más oszlopban más a feltételes megoszlás, hanem értelmet nyer az a kijelentés is, hogy nagyobb oszlopban a feltételes megoszlás úgy más, hogy inkább nagyobb sorbeli érték szerepelnek, vagy épp úgy, hogy inkább kisebbek. (Itt is egyenértékű, ha ugyanezt a sorok és oszlopok fordított szerepével mondjuk el.) Ezt ragadja meg a kapcsolat irányának fogalma: ha van kapcsolat (nem 0 az erőssége), akkor az pozitív, amennyiben az oszlopváltozó szerinti nagyobb érték tendenciájában a sorváltozó szerinti nagyobb értékkel jár együtt (és fordítva), negatív, ha az oszlopváltozó szerinti nagyobb érték tendenciájában a sorváltozó szerint kisebb értékkel jár együtt (és fordítva). Ordinális változónál erről is lehet nyilatkozni mutatókkal.

A konkrét mutatószámokkal most nem foglalkozunk (többek között azért sem, mert meglehetősen sok van belőlük, attól függően, hogy pontosan hogyan viselkednek az egyes változók).

3.5.2 Grafikus eszközök

Kontingenciatáblát vizualizálni ún. mozaikábrával és asszociációs ábrával lehet, ezek azonban nem túl látványos, és emiatt nem is túl gyakran használt módszerek, így most mi sem részletezzük ezeket.

Ami bevettebb, az a vetületi megoszlások (vagy nevezetes feltételes megoszlások) ábrázolása egyszerűen oszlopdiagramon (vagy kördiagramon), ez azonban jól láthatóan ugyanaz a feladat, amit már minőségi változók egyváltozós elemzésénél megbeszéltünk.

3.6 Mennyiségi változók kétváltozós elemzése

Mennyiségi változók kapcsolatát korrelációnak szokás nevezni a statisztikában. Erre jó példa adatbázisunk anyai testtömeg (lwt) és újszülött születési tömege (bwt) változói, melyek az anya illetve az újszülött testtömegét tartalmazzák.

3.6.1 Analitikus eszközök

A kapcsolat fogalmát mennyiségi változókra is ugyanazon gondolatot követve értelmezzük, mint amit minőségi változóknál már láttunk. Azt mondjuk, hogy két változó kapcsolatban van egymással, ha az egyik változó átlag feletti értékei tendenciájában a másik változó átlag feletti értékeivel járnak együtt (és ekkor persze fordítva is: az egyik változó átlag alatti értékei tendenciájában a másik változó átlag alatti értékeivel járnak együtt). Azaz: ha egy megfigyelési egység értéke az egyik változó szerint átlag feletti, akkor várhatóan a másik változó szerint is átlag feletti¹⁰ lesz. Pontosabban szólva ez a pozitív kapcsolat definíciója, a negatív esetén az egyik változó átlag feletti értékei tendenciájában a másik átlag alatti értékeivel járnak együtt, és fordítva. Itt természetesen sztochasztikus kapcsolatról beszélünk, ezért a ,,tendenciájában’’ kifejezés: nem arról van szó, hogy ha a megfigyelési egység egyik változója átlag feletti, akkor biztos, hogy a másik is, de az esetek többségében érvényesül ez a tendencia.

Érdemes megfigyelni, hogy itt mindenképp van értelme az iránynak (összhangban azzal, hogy a mennyiségi változók bírnak az ordinális tulajdonságaival is, természetesen).

Két mennyiségi változó fent definiált kapcsolatát klasszikusan a kovarianciával szokás lemérni. Ennek definíciója: \[ \mathrm{cov}\left(x,y\right)=\frac{\sum_{i=1}^n \left[\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)\right]}{n}. \] A számítás logikája vegytisztán tükrözi a definíciót: az $\left(x_i-\overline{x}\right)$ tükrözi az egyik, az $\left(y_i-\overline{y}\right)$ a másik változó szerint azt, hogy az adott megfigyelési egység átlag alatti vagy átlag feletti. Vegyük észre, hogy a kettő szorzata pedig pontosan akkor lesz pozitív, ha vagy mindkét változó szerint átlag feletti a megfigyelési egység, vagy mindkét változó szerint átlag alatti – azaz ha az adott megfigyelési egység a pozitív kapcsolatot erősíti meg! Ha a szorzat negatív, akkor az adott megfigyelési egység a negatív kapcsolatot erősíti.

Sőt, ennél több is igaz: a szorzatnak nem csak az előjele stimmel, de a nagysága is, az ugyanis kifejezi, hogy mennyire erősít meg bennünket az adott megfigyelési egység a kapcsolat fennállásában. Ha a megfigyelési egység egyik (pláne ha mindkét) változó szerint közel van az átlaghoz, akkor az csak gyenge ,,bizonyíték’’ a kapcsolat mellett (kis módosulással lehet, hogy az ellenkező irányú kapcsolatot erősítené), viszont ha mindkét változó szerint távol van az átlagtól, az erős érv a kapcsolat mellett.

A szummázás ezeket a hatásokat fogja összeadni megfigyelési egységről megfigyelési egységre, így előjele a kapcsolat irányát mutatja, abszolút értéke pedig annak erősségét. (Az $n$-nel való leosztás nyilván szükséges, különben a kétszer megismételt adatbázison kétszer akkora lenne a kovariancia, holott az információ ugyanaz; tehát ezeket a szorzatokat átlagolni kell.)

Hogy mi a kovariancia problémája, az azonnal kiderül, ha közöljük az anyai és az újszülött testtömeg közti kovarianciát: 4141.6518913. Ami kétségtelenül kiolvasható ebből, hogy az anyai és az újszülött testtömeg között van kapcsolat, mégpedig pozitív irányú (nagyobb anyai tömeg – nagyobb újszülött tömeg, és fordítva), hiszen az előjel pozitív. Amiről viszont lényegében semmit nem tudunk meg, az az erősség! Annál is inkább, mert a kovariancia mértékegység-függő: más értéket kapunk, ha az újszülött testtömegét nem grammban, hanem kilogrammban rögzítjük. Tekintetbe véve, hogy az információ ettől még ugyanaz marad, ez nyilván nem szerencsés A probléma tehát, hogy honnan tudhatnánk, hogy a 4141.6518913 sok vagy kevés? Ebben segít minket az a matematikai észrevétel, hogy mindenképp fennáll a $-s_x s_y \leq \mathrm{cov}\left(x,y\right) \leq s_x s_y$ összefüggés, tehát a kovariancia abszolút értéke nem lehet nagyobb mint a két változó szórásának szorzata. Így máris van mihez viszonyítani a kovariancia nagyságát! Ez tehát a következő mutató definiálását adja, a neve korrelációs együttható: \[ \mathrm{corr}\left(x,y\right)=\frac{\mathrm{cov}\left(x,y\right)}{s_x s_y}. \]

Ez az előjel értelmezésén semmit nem változtat, hiszen a kovariancia előjelét meghagyja (a nevezőben szórások szerepelnek, így mindkettő szükségképp pozitív), viszont az abszolút értéket értelmezhetővé teszi, hiszen a korrelációra már az teljesül, hogy $-1 \leq \mathrm{corr}\left(x,y\right) \leq 1$. A korreláció tehát minél közelebb van $\pm 1$-hez, annál erősebb a két változó közötti kapcsolat.

Például, az anyai testtömeg és az újszülött születési tömege közti korrelációs együttható értéke 0.1857333. Ez alapján nem csak azt tudjuk mondani, hogy van kapcsolat és az pozitív irányú (a 0.1857333 előjele pozitív), de most már azt is, hogy ez a kapcsolat igen gyenge (ha elhelyezzük a 0.1857333-ot a 0–1 között).

Belátható, hogy az így definiált korrelációs együttható a lineáris kapcsolat erősségét méri (szokás emiatt lineáris korrelációs együtthatónak is nevezni). Valóban, ha a korreláció abszolút érték 1, az épp azt jelenti, hogy $y=ax+b$ függvényszerű kapcsolat van a két változó között. De általában is, a korreláció ,,erősségét’’ úgy kell érteni, hogy mennyire szorosan valósul meg ez az egyenesre illeszkedés. Fontos megjegyezni, hogy más kapcsolat erősségét nem méri ez az együttható, tehát nem lineáris kapcsolat lehet a két változó között (extrém esetben akár függvényszerű is!), úgy, hogy közben a lineáris korrelációs együttható értéke nulla.

Erre tekintettel szokás más korrelációs együtthatókat is definiálni, ezek közül megemlítjük a Spearman-$\rho$ és a Kendall-$\tau$ mutatókat, ezek ún. rangkorrelációs mutatók, amik nem konkrétan lineáris, hanem általános monoton kapcsolat erősségét mérik. Nem foglalkozunk vele részletesen, de megemlítjük, hogy itt is igaz, hogy a kapcsolat erőssége azzal van összefüggésben, hogy az egyik változó ismerete mennyi információt árul el a másik változóról (természetesen sztochasztikus értelemben).

Végül egy figyelmeztetés. Mint általában, természetesen itt is elmondható, hogy a mutatószám használata nagyon nagy információtömörítést jelent. Éppen ezért ne támaszkodjunk önmagában egy korrelációs együtthatóra (és különösen ne önmagában egy lineáris korrelációs együtthatóra) két változó kapcsolatának megítéléséhez, hiszen ez elfedi az esetleges nemlineáris kapcsolatokat, az outliereket stb. Erre egy nevezetes példa az Anscombe-kvartett, amit mi is hamarosan bemutatunk.

3.6.2 Grafikus eszközök

Két mennyiségi változó kapcsolatának legfontosabb ábrázolási eszköze az szóródási diagram. A szóródási diagramot úgy kapjuk, hogy minden megfigyelési egységnek egy pontot feleltetünk meg a síkban úgy, hogy a pont egyik koordinátája a megfigyelési egység egyik, a másik koordinátája a másik változó szerinti értéke. (Tehát lényegében a megfigyelési egységhez tartozó változókat koordinátáknak tekintjük, és ezeket mérjük fel egy kétdimenziós koordináta-rendszer két tengelyére.) Az anyai és újszülött testtömeg szóródási diagramját @aref(fig:scatterplot). ábra mutatja.

plot( bwt ~ lwt, data = birthwt, xlab = "Anya testtömege (UM) [font]", ylab = "Születési tömeg [g]" )
abline( h = mean( birthwt$bwt ), v = mean( birthwt$lwt ), lty = "dashed" )
abline( lm( bwt ~ lwt, data = birthwt ), lty = "dotted" )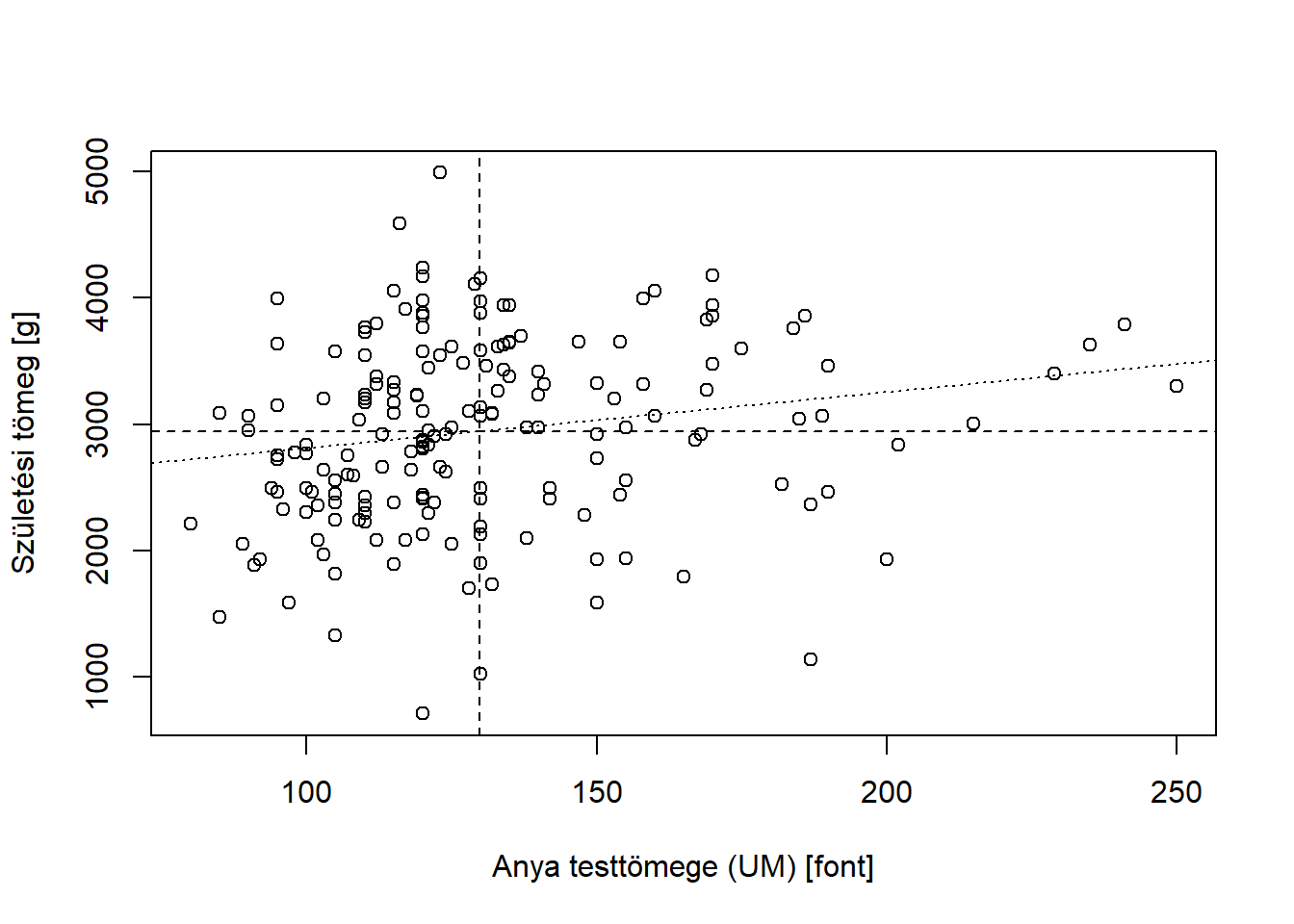

Ábra 3.6: Két mennyiségi változó kapcsolatának ábrázolása szóródási diagrammal.

Az ábrán bejelöltük (szaggatott vonallal, a két tengellyel párhuzamosan) a két változó átlagát is.

Jól látható, immár grafikusan is, hogy mit értünk a két változó közötti kapcsolat fogalmán: a pontok tendenciájukban a szaggatott vonalak által kijelölt koordináta-rendszer jobb felső és bal alsó kvadránsában találhatóak (átlag feletti – átlag feletti és átlag alatti – átlag alatti zónák). Természetesen látszik az is, hogy a kapcsolat sztochasztikus, azaz van pont a több kvadránsban is (itt aztán pláne, hiszen a kapcsolat nem is túl erős). Ne feledjük azt sem, hogy nem csak a pontok darabszáma számít, hanem a konkrét helyzetük is (mennyire ,,erősíti meg’’ a kapcsolat fennállását).

Ráerősítve az előbb mondottakra, az ábrán behúztuk a pontokra legjobban illeszkedő egyenest is. Ahogy említettük, a kapcsolat ,,erőssége’’ egyúttal azt is jelenti, hogy a pontok mennyire szorosan illeszkednek a rájuk legjobban illeszkedő egyenesre (látható, hogy itt nem túl szorosan).

Mindezeket szemlélteti @aref(fig:corrdemo). ábra is, mely különböző korrelációs együtthatójú kapcsolatokat (különböző előjelekkel és abszolút értékekkel, azaz különböző irányú és erősségű kapcsolatokat) mutat be példákkal.

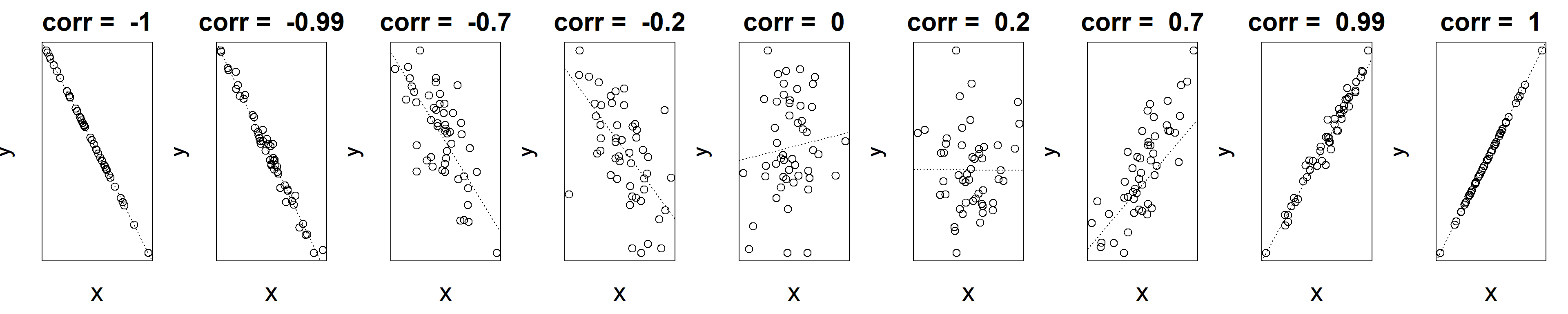
Ábra 3.7: Különféle korrelációs együtthatók szemléltetése.

A grafikus ábrázolás előnye, hogy (szemben a korrelációs együtthatóval) nem okoz gondot semmilyen outlier, nemlineáris kapcsolat stb. – ezek mind láthatóak lesznek az ábrán. (Itt is hangsúlyosan él tehát Tukey már említett tanácsa) Erre mutat példát a nevezetes Anscombe-kvartett (3.8. ábra). Az ábrák négy kétváltozós adatsor szóródási diagramját mutatják. Mindegyiknek hajszálpontosan ugyanaz a korrelációs együtthatója (sőt, az átlaguk és a szórásuk is – így ugyanaz a rájuk legjobban illeszkedő egyenes is), mégis, a valós helyzet drámaian más. Outlierek, nemlineáris kapcsolatok vannak jelen. Ez azonban csak ábrázolás után derül ki, a korrelációs együttható használata mindezt teljesen elfedné!

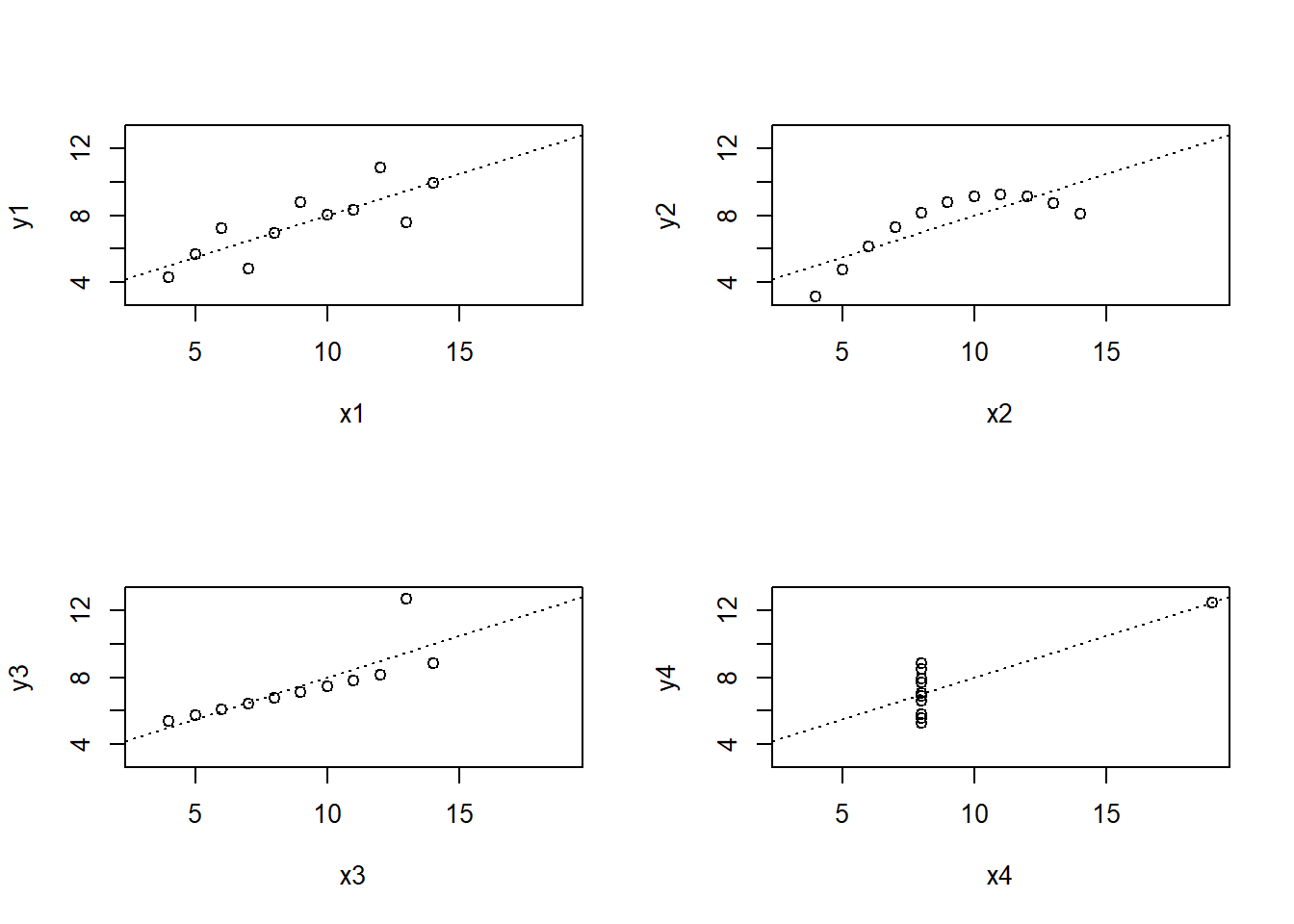
Ábra 3.8: Az Anscombe-kvartett.

Zárásként megjegyezzük, hogy ebben a grafikus ábrázolásban valóban nincsen semmilyen információtömörítés. Az is igaz, hogy a kétváltozós elemzés tartalmaz minden információt, amit a két egyváltozós elemzés: a pontokat levetítve valamelyik tengelyre, visszakapjuk az adott tengely változójának adatait; azokat csoportosítva (a tengelyt osztályközökre bontva) rögtön készíthető például hisztogram. Szemléletesen látszik azonban az is, hogy pusztán a hisztogramokból (tehát az egyváltozós adatokból) lehetetlen lenne nyilatkozni a két változó közti kapcsolatról. (Képzeljünk egy egy olyan esetet, melyben a változók között erős kapcsolat van, de úgy, hogy mindkét változó önmagában szimmetrikus. Ekkor nyugodtan tükrözhetnénk a szóródási diagramot bármelyik átlagot jelentő szaggatott vonalra, az egyváltozós adatok ugyanazok maradnának, noha kétváltozósan pont hogy megfordult a kapcsolat iránya.) Ezért több a kétváltozós elemzés mint két egyváltozós elemzés.

3.7 További többváltozós elemzések

A kétváltozós esetek tárgyalásából a fentiekben kimaradt az az eset, amikor egy minőségi és egy mennyiségi változó kapcsolatát kell vizsgálni. Ezt vegyes kapcsolatnak szokás nevezni; részletesebben most nem foglalkozunk vele.

A másik kérdés, ami felmerül, hogy mi a helyzet kettőnél több változó esetén. Ha nem lényegesen több változóról van szó, akkor a fenti módszerek – több-kevesebb módosítással – de kiterjeszthetőek. Például a szóródási diagram elvileg három változós esetre változatlanul kiterjeszthető (bár a gyakorlatban már ezt sem nagyon szokták használni, hiszen egy három dimenziós pontfelhő csak számítógépen tekinthető meg érdemben, és ott se túl áttekinthető emberi szemnek). Négy és annál több dimenziónál már trükkre van szükség; a tipikus megoldás, hogy minden lehetséges koordináta-párra levetítik a sokdimenziós pontfelhőt, és az így kapott kétdimenziós szóródási diagramokat mutatják meg (mátrix szóródási diagram). Egy-két tucat változó felett azonban már ez sem igazán tekinthető át, illetőleg már nem nevezhető érdemben kettőnél több dimenziós elemzésnek. Hasonló a helyzet a korrelációs együtthatóval, illetve a kontingenciatáblával és elemzési eszközeivel.

Most még nem fontos, hogy ezek a mutatók pontosan mit jelentenek (a későbbiekből úgyis ki fog derülni), csak annyi számít, hogy a minta különböző leírói.↩︎
E jelenséget később pontosabban is meg fogjuk ragadni, de most bőven elég lesz ez a kissé pontatlan megfogalmazás is.↩︎
Vö. mode (angol), die Mode (német) a.m. divat; a szó egyébként a hasonló értelmű francia kifejezésből jön.↩︎
Ebből a kötöttségből még egy dolog következik: lesz értelme beszélni arról is, hogy mennyi a gyakoriság egy adott kategóriáig. (Nem csak adott kategóriában.) Ez nyilván értelmetlen fogalom mindaddig, amíg a kategóriák között nem értelmeztünk sorrendet. Éppen ezért ekkor bevezethető a kumulált gyakoriság fogalma (jele $f'$), mely adott kategóriára nem más, mint a gyakoriságok összege az adott a kategóriáig. (A szokásos definíció szerint: azt is beleértve.) Tehát formálisan: $f'_i=\sum_{j:C_j\leq C_i} f_j$. Hasonlóképp beszélhetünk kumulált relatív gyakoriságról (jele $g'$), mint a relatív gyakoriságok összege adott kategóriáig (azt is beleértve), tehát formálisan $g'_i=\sum_{j:C_j\leq C_i} g_j$. Nyilván $f'_{\max_j C_j}=n$ és $g'_{\max_j C_j}=1$.↩︎
Emlékezzünk vissza, hogy a magasabb mérési skála minden alacsonyabb tulajdonságával bír, így természetesen az összes, alacsonyabb mérési skálán értelmezett módszer a magasabb mérési skálák esetében is alkalmazható.↩︎
Így már az is érthető, hogy a trimmelt átlag egyfajta kompromisszumnak tekinthető a kettő között, ti. a robusztusság és a mintaértékek mind teljesebb kihasználása között. Az is észrevehető, hogy bizonyos értelemben ez ráadásul általánosítja is a két mutatót: a 0%-os trimmelt átlag épp a ,,hagyományos’’ átlag, a 100%-os trimmelt átlag pedig épp a medián.↩︎
Két dolgot érdemes ennek kapcsán megjegyezni. Az egyik, hogy az előzőek fényében a vetületi megoszlásokat joggal nevezhetjük (precízebben) a változó feltétel nélküli vetületi megoszlásának. A másik, hogy jobban belegondolva észrevehető, hogy az elsőként definiált ,,szokásos’’ relatív gyakoriság is ,,gyakoriság / peremgyakoriság’’ alakú (tehát megoszlás), csak épp a peremgyakoriság nem fenti ,,egyszerű’’ (egydimenziós) peremgyakoriság, hanem a peremgyakoriságok peremgyakorisága (egyfajta nulladimenziós peremgyakoriság). Ezt szokás együttes megoszlásnak nevezni (szemben az eddig definiált feltételes megoszlással, és a feltétel nélküli, de vetületi megoszlással).↩︎
Az átlag itt természetesen minden esetben a szóban forgó változó átlagát jelenti. A használatára azért van szükség (és azért nem mondhatjuk egyszerűen azt, hogy ,,a változó nagy értékei’’), mert hozzáadva valamilyen nagy konstanst a változóhoz, annak összes értéke nagy lesz, tehát mindenképp valamilyen viszonyításra van szükség.↩︎