6. fejezet Végpont és lemérése

Megbeszéltük, hogy a végpont a számunkra érdekes kimenet, például, hogy a beteg infarktust kap. De hogyan lehet ennek a kockázatát számszerűsíteni, és hogyan lehet gyógyszer ezt csökkentő (vagy ártalmas expozíció ezt növelő) hatását egyetlen számban kifejezni?

A hatás számszerű „lemérése” ugyanis ezt jelenti: hogyan tudjuk egy számba sűríteni azt, hogy az adott expozíció hogyan változtatja a kockázatot? Az egyszerűség kedvéért szorítkozzunk most egyetlen esetre, mely a gyakorlatban is az egyik legfontosabb és egyúttal az általános jelenségek is jól illusztrálhatóak rajta: arra, ha a végpont két lehetséges kimenetet vehet fel, úgy is szokták mondani, bináris vagy dichotóm. Ilyen az, hogy az alany meghalt-e adott időn belül, rákos lett-e, mentális beteg lett-e, és így tovább. Hogy egyéb problémákkal ne bonyolítsuk a kérdést, mondjuk, hogy két összehasonlított csoport van (exponált és nem exponált: gyógyszert kapó a gyógyszert nem kapóval szemben, légszennyezett területen élő a nem légszennyezett területen élővel szemben és így tovább), valamint, hogy nincs confounding, egy tökéletesen kivitelezett kísérletet végeztünk.

Az első megállapítás, hogy ebben az esetben a kockázat egy arány: a csoportból az alanyok mekkora hányada érte el a végpontot, például hány százalék kapott adott időn belül infarktust. A „hatás lemérése” tehát azt jelenti, hogy két arányt kell összevetnünk: ha 100 exponáltból 1 érte el a végpontot, akkor 1% az egyik arány, ha a nem exponált 200 főből 4, akkor 2% a másik. Na de mit értünk összevetés alatt? Ennek megválaszolása mondja meg, hogy hogyan mérjük le a hatást. Az érdekes az, hogy még ebben az elképzelhető legegyszerűbb helyzetben (egyetlen bináris végpont, két csoport) is nagyon nem nyilvánvaló problémákra vezet ez a kérdés…!

6.1 Mikor adjunk gyógyszert?

A konkrétság kedvéért mondjuk, hogy egy koleszterinszintet csökkentő gyógyszert vizsgálunk, a végpont, hogy az alany infarktust kap-e adott időn belül. Azt tapasztaljuk, hogy a gyógyszerrel kezelt csoportban egy év alatt 1% kap infarktust, a gyógyszert nem kapó kontrollcsoportban 2%. Akkor most mit mondunk?

1. A fantasztikus gyógyszerünk 50%-kal csökkenti az infarktus-rizikót!

2. A fantasztikus gyógyszerünk nélkül 100%-kal nagyobb az infarktus-rizikó!

3. Ezzel a gyógyszerrel 100 embert kezelve 98-at feleslegesen kezelünk (hiszen gyógyszer nélkül sem kapna infarktust), 1-et hiába kezelünk (hiszen a gyógyszerrel együtt is infarktust kap), és 1 az, akinél elérünk valamit. Miközben mind a 100-at kitesszük a mellékhatások kockázatának és mind a 100-zal kifizettetjük a gyógyszert.

Ugye mennyire máshogy hangzik? Pedig csak osztani kell tudni, hogy lássuk: ez a három igazából ugyanaz!

A fenti példák rámutatnak a hatás lemérésnek két alapvető lehetőségére: arra, ha a két arányt elosztjuk egymással (ezt szokás relatív rizikónak nevezni), és arra, ha kivonjuk őket egymásból (abszolút rizikó-különbség). Ha osztunk, akkor kapjuk az első két megfogalmazást (pl. 1%/2%=0,5, amit úgy is kifejezhetünk, hogy -50%), ha kivonunk, akkor a harmadikat (2%-1%=0,02-0,01=0,01=1 %pont, ami épp az 1 a 100-ból).

Az első tanulság a fentiekből, hogy a racionális gyógyszerelés alapját az abszolút mutató jelzi. Szemben azzal, amit esetleg elsőre gondolhatna az ember, hogy ti. a gyógyszer adásának mérlegelésekor a gyógyszer mellékhatásait kell a megelőzni kívánt végpont szövődményeivel összevetni, a fenti mutatja, hogy valójában a gyógyszer mellékhatásait be kell szorozni 100-zal, és úgy hasonlítani az infarktushoz! Hiszen 100 embert kell kitenni ezeknek ahhoz, hogy egyetlen infarktust megelőzzünk. Egy következmény azonnal látható: ritka betegségek megelőzésére csak nagyon biztonságos gyógyszerek használhatóak. (A nem megelőző, hanem gyógyító jellegű készítmények pedig végképp előnyben vannak ilyen szempontból, hiszen ott nem kell arra tekintettel lenni, hogy kezelés nélkül sem biztos, hogy baja lesz az alanynak.) A klinikai döntéshozatal szempontjából tehát az abszolút hatás a mérvadó. De akkor miért használjuk egyáltalán a relatív mutatókat?

6.2 Kísérletek résztvevői, avagy végre kiderül, hogy jót tesz-e repülőgépből kiesésnél, ha van nálunk ejtőernyő

Kezdjük a kérdést egy picit messzebbről! Korábban már volt róla szó, hogy a klinikai kísérleteknek, azon hatalmas előny mellett, hogy teljes mértékben védettek tudnak lenni a confoundinggal szemben, három, helyzettől függően kisebb vagy nagyobb hátrányuk van. Az egyik, hogy korlátozott az elérhető mintanagyság – emiatt kicsi hatásokat (kis mértékű, vagy keveseket érintő hatásokat), legyen szó akár pozitív hatásról, akár mellékhatásról, nem tudunk észrevenni. A második, az előzőhöz nagyon hasonló limitáció, hogy korlátozott az utánkövetési idő, ezért a lassan fellépő hatásokat nem tudjuk észrevenni.

A harmadikról azonban eddig még nem beszéltünk részletesen: arról, hogy a klinikai kísérletekben részt vevő betegek jellemzői szinte mindig eltérnek, néha nem is kicsit, a betegek összességének jellemzőitől. Nevesítve: a klinikai kísérletekben részt vevő betegek legtöbbször fiatalabbak, mint általában véve a betegek, több köztük a férfi, ritkábbak a társbetegségek. De miért van ez így?

A jelenségnek vannak jóhiszemű és kevésbé jóhiszemű magyarázatai. Az első szűrő kapásból az, hogy bár a történelemben ez sajnos nem volt mindig így, de manapság már a klinikai kísérletekben kizárólag önkéntesek vesznek részt. Ez azt jelenti, hogy még ha a felkért betegek tökéletesen meg is felelnek összetételben az összes betegnek, azok akik vállalják a részvételt már rögtön nem fognak, hiszen az önkéntesség önmagában jelent eltérő jellemzőket (például a férfiak inkább hajlandóak kipróbálni ilyen kockázatos dolgokat). Ezzel pedig lehetetlen bármit is kezdeni, hiszen az az önkéntesség megsértését jelentené. A valóságban ráadásul a felkért betegek köre már önmagában is eltérő lesz: az ilyen klinikai kísérleteket tipikusan nagy, magas szinten lévő, városi centrumok végzik; az önmagában sokszor szűrés, például szocioökonómiai státusz szerint, hogy egyáltalán ki az, akit ilyen centrum lát el. A végeredmény az, hogy simán előfordulhat, például kardiológiában, hogy egy kísérletben a – „standard ellátást” kapó – kontrollcsoport halálozása fele az országos adatnak! Mindezek tetejébe jönnek a bevonási és kizárási kritériumok, ezek határozzák meg, hogy milyen betegek vehetnek részt a kísérletben, és kik azok, például életkor, társbetegségek, kórelőzményi adatok vagy épp súlyosság szerint, akik nem. Itt megjelennek a kevésbé jóhiszemű szempontok is: a szponzornak (a szakzsargonban így szokták hívni a kísérlet finanszírozóját) gyakran érdeke, hogy olyan betegek kerüljenek be, akiknek a legjobb a gyógyhajlama, hogy a vizsgált szer a legjobb színben tűnhessen fel. Erre pedig a bevonási és kizárási kritériumok meghatározásán keresztül lehet ráhatásuk.

Csak egyetlen példa mindezek eredőjének illusztrálására: Travers és munkatársai egy emlékezetes 2007-es cikkükben véletlenszerűen kiválasztott, „való életbeli” asztmás betegeknél nézték meg, hogy milyen gyógyszereket szednek a betegségükre, és hogy azokat a gyógyszereket milyen bevonási és kizárási kritériumú kísérletek alapján törzskönyvezték. Ezután összevetették a betegek adatait e kritériumokkal, és megnézték, hogy mekkora hányaduk vehetett volna részt az egyes kísérletekben; íme a százalékok: 5, 7, 6, 6, 0, 4, 2, 1, 7, 8, 7, 36, 2, 1, 1, 2 és 3. Látható, hogy egyetlen kísérlet volt, ahol legalább a kétszámjegyű százalékot sikerült elérni, egyébként az 1-3% a tipikus, de a legjobb, hogy olyan kísérlet is volt, aminél konkrétan nem találtak élő beteget, aki jogosult lett volna részt venni benne… Amiben ugye az a vicces, hogy utána a betegeket kezelik azokkal a gyógyszerekkel, amiket ilyen kísérletek alapján törzskönyveztek!

Ezek az arányok egyáltalán nem kiugróak, számos területen tapasztalható, hogy éves nagyságrendben kell várni, hogy elég beteg összegyűljön, mivel 80, 90 vagy annál is nagyobb százalékuk nem jogosult a részvételre. Ezt a jelenséget hívják szelekciós torzításnak; szokás beszélni a kísérlet külső validitásáról vagy általánosíthatóságáról is, hiszen a probléma az, hogy bármit is találunk a kísérletbe bevont alanyok csoportján belül, az vajon mennyire vonatkoztatható az összes betegre általában. Így már talán még jobban érthető, hogy miért mondtuk annak idején, hogy ez a megfigyeléses vizsgálatok egyik előnye: ott sokkal kevésbé kell aggódnunk azon, hogy az eredmények mennyire vonatkoztathatóak az összes betegre, hiszen nem ritka, hogy akár az összes beteg is bevonható a vizsgálatba.

Ha már a korábban mondottaknál tartunk: talán emlékszik a nyájas Olvasó, hogy a tudomány jelen állása szerint nem tudhatjuk „biztosan”, hogy jót tesz-e, ha van nálunk ejtőernyő amennyiben kiesünk egy repülőgépből, legalábbis ha a biztosan alatt azt értjük, hogy „kísérlettel megvizsgálva”. Hivatkoztam is Smith és szerzőtársa cikkére, mely az igen tekintélyes British Medical Journal 2003-as karácsonyi számában jelent meg, és amelyikben rendkívül alapos kutatással feltárták, hogy egyetlen egy ilyen kísérletet sem végeztek! (Nyilván gúnyolódva azokon, akik a kísérleteket mindenhatónak állítják be.) Nos, jelenthetem, hogy az orvostudomány fejlődése megállíthatatlan, ugyanis a helyzet azóta megváltozott! A British Medical Journal-ben a napokban, egész pontosan december 13-án, természetesen csak teljes véletlenségből megint a karácsonyi különszámban megjelent a történelem első kísérletes vizsgálata, amely az ejtőernyő hatásosságát vizsgálta! A kísérlet alanyai tökéletesen randomizáltan kaptak vagy ejtőernyőt, vagy ejtőernyőt nem tartalmazó hátizsákot, ezt követően kiugrottak a repülőgépből, majd a kutatók rögzítették a földbe csapódáskor fellépő halálozások, illetve súlyos sérülések (a traumatológiában általánosan használatos ISS sérüléssúlyossági pontszám 15-nél nagyobb) fellépését. A kísérlet igen gondos tervezésű volt, az előző részben látott módon határozták meg a mintanagyságot, rögzítettek számos fontos betegjellemzőt, még arra is ügyeltek, hogy a felhasznált ejtőernyők, sőt, hátizsákok típusát és gyártóját dokumentálják, beszerezték az etikai engedélyt a kísérletre stb. Egyszóval egy minden elvárásnak megfelelő kutatásról van szó. Hadd fussak előre: a vizsgálat szerint az ejtőernyő nem csökkentette a földet éréskor bekövetkező halálozások és súlyos sérülések számát!

Hogy ezt miért pont most, a klinikai kísérletek résztvevőinek speciális összetételéről szóló résznél mondom? Ehhez érdemes közelebbről megnézni a kísérlet pontos lefolytatását!

A részvételre felkért alanyok két csoportból kerültek ki: egy részüket sugárhajtású repülőgépen repülés közben interjúvolták meg, hogy vállalják-e a kiugrást randomizáltan ejtőernyővel vagy hátizsákkal, más részüknek repülőgép-múzeumban, egy földön álló kisrepülőben tették fel ugyanezt a kérdést (6.1. ábra). A fent említett eredményhez talán azt a mellékes információt érdemes hozzátenni, hogy az előbbi csoportból 0% vállalta a részvételt, míg az utóbbiak közül 100% (erre nincs ráhatásunk, önkéntesség, ugyebár!), így apróbb eltérések keletkeztek a klinikai kísérletbe bekerülő és be nem kerülő alanyok között: az utóbbiak esetében a repülőgép átlagos sebessége 800 km/h volt, az előbbieknél 0 km/h, az utóbbiaknál az átlagos ugrási magasság 9146 méter, az előbbieknél 60 centiméter…

6.1. ábra. Reprezentatív példa a kísérletben részvételt vállaló alanyra (kontroll – hátizsák – csoport). Fontos megjegyezni, hogy a képen látható alany nem halt meg, illetve nem szenvedett súlyos traumás sérülést a földbe csapódáskor.

Az említett eredmény úgy jött ki, hogy mind az ejtőernyős csoportban, mind a kontrollcsoportban 0 halálozás, illetve súlyos sérülés fordult elő. Tehát: nincs különbség…

Nagyon fontos újra hangsúlyozni, hogy a kísérlet szervezői mindenféle kockázatnak kitett alanyt igyekeztek verbuválni, arról már nem tehetnek a szerzők, hogy történetesen a részvételt vállalók köre „némileg” speciálisra sikeredett – és pont arra akarják felhívni a figyelmet, hogy ez egy valódi klinikai kísérletben is előfordulhat. Zárásként adjuk vissza a szót a szerzőknek: „a magas kockázatnak kitett alanyok részvételének a hiánya elképzelhető, hogy befolyásolta a vizsgálat végeredményét”.

6.3 Mutatók stabilitása

Egy dolog azonban még mindig lóg a levegőben: mi köze ennek a relatív és abszolút mutatókhoz? Bármilyen furcsa is lehet elsőre, de nagyon sok: ha relatív mutatót használunk, az az egész fenti problémát sok esetben meg tudja oldani, vagy legalábbis jelentősen enyhíti!

A klinikai kísérletekben fiatalabbak az alanyok, kevésbé súlyos az állapotuk, kevesebb társbetegségük van? Igen. Emiatt jobb a gyógyhajlamuk, mint a betegeknek általában? Igen. Csakhogy mi, ha relatív mutatót használunk, akkor nem is ezt nézzük, hanem azt, hogy egymáshoz képest hogyan viselkednek a kezelt- és kontrollcsoportok! Igen, fiatalabbak, de a kezelt és a kontrollcsoport egyaránt fiatalabb, márpedig őket egymáshoz hasonlítjuk! Lehet, hogy a klinikai kísérletben 10% a halálozás a kontrollcsoportban, míg a valóságban 20, de ha ez 8-ra megy le a kezelés hatására, akkor reménykedhetünk benne, hogy a 20 meg 16-ra fog. Igen, a klinikai kísérlet betegeinek összetétele eltérő volt, ezért a halálozási arányok is mások voltak, de a relatív viszonyok állandóak! Ha ez igaz, tehát a relatív mutató stabil, akkor onnantól nem is annyira számít, hogy a klinikai kísérlet betegei tényleg speciális populációt jelentenek-e, hiszen mi úgysem az abszolút számokat fogjuk felhasználni, hanem a relatív viszonyokat – ami viszont a nem speciális populációra is érvényes.

De tényleg stabilak a relatív mutatók? A tapasztalatok szerint igen! Fontos előrebocsátani, hogy ez nem valamiféle matematikai törvényszerűség, és nincs is rá garancia, hogy mindig teljesüljön (épp emiatt még ennek fényében is igenis hasznos, ha a klinikai kísérlet alanyai nem nagyon speciálisak!), de nagy általánosságban véve a relatív mutatók meglepően stabilak. Erre mutat példát a következő táblázat egy koleszterinszintet csökkentő gyógyszercsalád néhány kísérletének példáján keresztül.

Kísérlet neve	Kontrollcsoport rizikója	Relatív rizikó	Abszolút rizikó-különbség	Utánkövetés hossza [év]
JUPITER	0,48%	0,81 (-19%)	0,09 %pont	1,9
AFCAPS/TexCAPS	0,76%	0,68 (-32%)	0,24 %pont	5,2
ASCOT-LLA	1,60%	0,90 (-10%)	0,16 %pont	3,3
WOSCOPS	2,22%	0,68 (-32%)	0,70 %pont	4,9
CARE	6,26%	0,86 (-14%)	0,87 %pont	5,0
HPS	9,13%	0,83 (-17%)	1,52 %pont	5,0
4S	9,31%	0,66 (-34%)	3,19 %pont	5,4
LIPID	9,62%	0,76 (-24%)	2,28 %pont	6,1
PROSPER	10,06%	0,86 (-14%)	1,38 %pont	3,2

1. táblázat – Különböző kísérletek, melyben a sztatinnak nevezett koleszterinszint-csökkentő készítmények hatását vizsgálták. A táblázat a szív-érrendszeri eredetű halálozások arányát mutatja a kísérlet utánkövetése alatt. Az utolsó oszlop az utánkövetési idő hossza (átlag vagy medián, függően attól, hogy a tanulmány mit közölt).

Gyönyörűen látható, hogy a gyógyszereket nagyon-nagyon különböző populációkban próbálták ki: volt, ahol csak 0,48% halt meg szív-érrendszeri okból a kontrollcsoportban, de volt, ahol több mint húszszor ennyi. (Ez a kezelés nélküli rizikó, ez jellemzi tehát, hogy milyen alanyok körében végezték a kísérletet.) Az abszolút rizikó-különbség ennek megfelelő drámai eltéréseket mutat, a legkisebb és a legnagyobb között több mint harmincötszörös a különbség. Igen ám, de – és most jön a lényeg – mindeközben a relatív hatás bámulatosan állandó, 10 és 30% közötti kockázatcsökkenés látható függetlenül attól, hogy milyen kockázatú populációban végezték a vizsgálatot! Az elsőként felsorolt kísérletet olyan populációban végezték, hogy kezelés nélkül fél százalék halt meg, az utolsót olyanban, ahol több mint 10, de a gyógyszer relatív hatása alig tér el!

Mindezeket úgy is elmondhatjuk: a jelek szerint a gyógyszerre saját magára jellemző tulajdonság a relatív hatás, az az, ami állandó. Az abszolút hatás egy származtatott mutató, egy eredő: a (gyógyszerre jellemző) relatív hatás, és az (adott populációra jellemző) kockázat szorzata. A relatív hatás állandó, az abszolút hatás attól függ, hogy mennyi a kezelés nélküli kockázat: ahol nagy (pl. idős, sok társbetegséggel rendelkező beteg), ott az abszolút csökkenés is nagy lesz, ahol kicsi, ott kicsi (6.2. ábra).

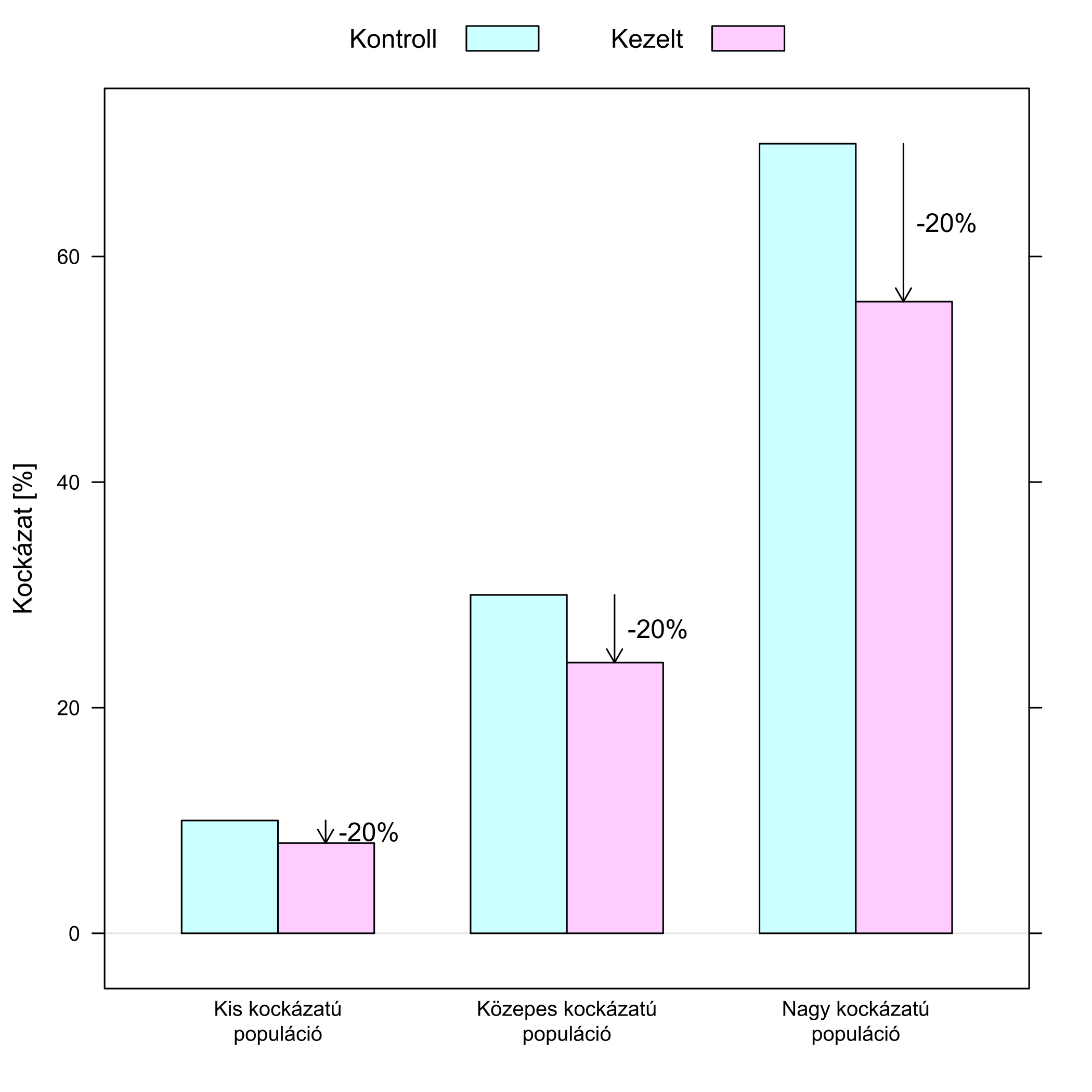
6.2. ábra. Ugyanolyan (20%-os) relatív csökkenés abszolút hatása attól függ, hogy honnan indulunk: minél nagyobb a kezelés nélküli kockázat, annál nagyobb abszolút különbség tartozik ugyanakkora relatív csökkenéshez.

Ennek két nagyon fontos következménye van. Az egyik, hogy egy kísérlet eredményének megadásakor igenis jogos a relatív mutató használata, hiszen egy gyógyszerkísérletben értelemszerűen azt kell kimérni, ami magára a gyógyszerre jellemző. A másik, hogy ez persze nem változtat azon, hogy a klinikai döntéshozatal szempontjából az abszolút különbség a mérvadó. Sőt, ez rögtön érthetővé teszi, hogy miért van az, hogy egy fiatal, terhelő kórelőzmény nélküli, egyébként egészséges betegnek lehet, hogy nem ilyen gyógyszert fog felírni az orvos, míg egy idős, korábban szívinfarktuson átesett, cukorbeteg páciensnek igen – nem azért, mert azt gondolná, hogy az előbbi esetben nem hat a gyógyszer, az utóbbi esetben viszont igen. Könnyen lehet, hogy pontosan ugyanúgy hat a gyógyszer, azaz pontosan ugyanúgy 20% kockázatot csökkent, csakhogy ez a -20% az előbbi esetben, mivel alacsonyról indulunk, nagyon kis abszolút kockázatcsökkenés (és így a gyógyszer mellékhatásai nagyobb súllyal esnek latba), míg az utóbbi esetben fordított a kockázat/haszon mérleg.

A kettőt összerakva láthatjuk, mi a helyes eljárás: a kísérletben azt kell kimérni, ami stabil és ami a gyógyszerre jellemző, aztán ezt az információt a konkrét klinikai alkalmazásban kontextusba kell helyezni. Azaz: a – kísérletből ismert, gyógyszerre jellemző – relatív mutatót az adott konkrét beteg jellemzői, például társbetegségei vagy életkora alapján át kell számolni abszolút mutatóra… és ez alapján dönteni!

Most, hogy mindent értünk, némileg a legelső példa is újraértékelhető. Abból ugyanis nem került ki túl jól a gyógyszer (100 beteget kellett kezelni egy infarktus elkerüléséhez), de nézzük csak meg a számokat: 2% infarktusrizikó még kezelés nélkül is? Miközben Magyarországon 15 ezer ember kap infarktust – minden egyes évben! Ez meg hogyan lehet? Az 1 és 2% persze nyilván kerek szám volt a példa kedvéért, de ha megnézzük a táblázatot, nagyságrendileg nem tévesek, tényleg van számos nemzetközi kutatás ilyen számokkal (pedig máshol sem sokkal kisebb az infarktus-rizikó). A választ akkor kapjuk meg, ha ránézünk a táblázat jobb szélső oszlopára is: e kutatások utánkövetési ideje mindössze néhány év volt! Az infarktus-rizikó azonban nemhogy több év, hanem inkább évtizedek alatt épül fel, e gyógyszereket is ilyen távon szedik igazából a betegek. E kutatásokat tehát nem lehet a valós helyzetre közvetlenül rávetíteni… illetve nem lehetne, ha nem lenne a relatív rizikó! Ugyanis a kis kockázatú populáció nem csak azt jelentheti, hogy fiatal meg nem cukorbeteg, hanem azt is, hogy kevés ideig utánkövetett, a nagy kockázatú meg nem csak az idős és cukorbeteg lehet, hanem a realisztikus ideig utánkövetett. Az előző megállapításunk tehát azt mondja ez esetben, hogy a kísérletből ne az abszolút kockázatot olvassuk ki, hiszen az rövid utánkövetésre vonatkozik, nem a valóságra. Olvassuk ezzel szemben ki a relatív kockázatot, hiszen az stabil (reményeink szerint a különböző utánkövetési időkre nézve is!), és azt használjuk: számítsuk át, hogy mi történne hosszabb, azaz a valóságnak megfelelő utánkövetési idő alatt. A példa 1 éves utánkövetést írt; kiszámítható, hogy 5 év alatt a kontrollcsoport kockázata már 9,6%, nem 2%. Ha a -50% állandó marad, akkor az abszolút különbség máris 4,8 %pont, nem 1 %pont – 21 embert kell kezelni egy infarktus megelőzéséhez. 10 év alatt a kockázat 18,3% (látszik, hogy szépen közeledünk a valós kockázatokhoz!), a gyógyszer abszolút hatása 9,1 %pont csökkenés – 11 embert kell kezelni egy infarktus megelőzéséhez, azaz már csak 11-gyel kell szorozni a gyógyszer mellékhatásait a kockázat/haszon mérlegelésnél. Máris máshogy hangzik!

6.4 Döntéshozatal és az abszolút és relatív mutatók

Vajon hogyan használhatóak a különböző mutatók arra, hogy jobban megértsük, mi a helyes döntés egy beteg ellátása során? A statisztika természetesen nem tudja átvenni az orvosi döntéshozatal szerepét, de hatalmas segítséget adhat annak megalapozottabbá tételében, azáltal, hogy a választási lehetőségeket jobban megértjük.

Érdemes a kiindulópontunkat felidézni: egy gyógyszer az infarktus kockázatát 2%-ról 1%-ra csökkenti. Ha azt mondjuk, hogy „50%-kal csökkenti az infarktusrizikót”, akkor relatív mutatóval írtuk le a hasznosságát, ha azt mondjuk „1%ponttal csökkenti az infarktusrizikót”, akkor abszolút mutatót használtunk. Megbeszéltük, hogy az előbbi mutatót érdemes klinikai kísérletben kimérni, mert stabilabb: azt reméljük, hogy az 50%-os csökkenés az, ami magára a gyógyszerre jellemző, és így állandó marad akkor is, ha a kezelés nélküli kockázat nem 2%. Ez tehát azt jelenti, hogy a relatív mutatók használata lehetővé teszi a klinikai kísérlet eredményeinek az általánosítását: ha a rendelőnkben ülő beteg kockázata nem 2% hanem 10%, akkor is tudjuk, hogy mire számíthatunk – arra, hogy ezt 5%-ra csökkenti a gyógyszer.

Az abszolút mutatóról azt mondtuk, hogy ez fontos a klinikai döntéshozatalhoz, például annak eldöntéséhez, hogy adjunk-e ilyen gyógyszert a betegnek. Ennek logikáját érdemes részletesen is felidézni: a fenti számok azt jelentik, hogy ezzel a gyógyszerrel 100 embert kezelve 98-at feleslegesen kezelünk (hiszen gyógyszer nélkül sem kapna infarktust), 1-et hiába kezelünk (hiszen a gyógyszerrel együtt is infarktust kap), és 1 az, akinél elérünk valamit – miközben mind a 100-at kitesszük a mellékhatások kockázatának. Ez az „1 a 100-ból” épp az abszolút mutató 1%pontja. Az, hogy 100 beteget kell kezelnünk 1 végpont megelőzéséhez, azért nagyon fontos, mert így már látható, hogy mit kell mérlegelnünk, ha racionálisan akarunk dönteni a gyógyszeradásról: azt, hogy mi a rosszabb, az infarktus szövődményei, vagy a gyógyszer mellékhatásai beszorozva 100-zal! Érthető tehát, hogy miért mondhatjuk, hogy ez mutatja a gyógyszer klinikai előnyét, miért ez a releváns a döntéshozatalhoz: ha a betegünk kockázata kezelés nélkül 10%, akkor az abszolút előny 5%pont, tehát nála már csak 20-szal kell szorozni a gyógyszer mellékhatásait a kockázat/haszon mérlegelés során.

Azonban nem ez az egyetlen terület, ahol az abszolút mutatók jól jönnek.

Elsőként kezdjünk egy kis ismétléssel; hogy látványosabb legyen a dolog, nézzünk egy konkrét, való életbeli példát! Lipson és szerzőtársai egy 2018 májusában megjelent cikkükben a krónikus obstruktív tüdőbetegség (továbbiakban röviden: COPD) kezelési lehetőségeit vizsgálták. A COPD, amely elsősorban a dohányosok betegsége, a légutak beszűkülésével és a tüdő szövetének pusztulásával járó visszafordíthatatlan, folyamatosan súlyosbodó gyulladásos folyamat. Ebben a betegségben az egyik dolog, amitől félünk, az a nagyon hirtelen kezdődő, átmeneti állapotrosszabbodás. Ez sajnos időről-időre előfordul a COPD-s betegeknél, és egyrészt – különösen a rosszabb állapotú alanyoknál – akár nagyon súlyos lefolyású is lehet, másrészt még ha nem is történik nagy baj, a beteg későbbi kilátásait akkor is rontja minden egyes ilyen epizód. Éppen ezért nem meglepő, hogy a gyógyszeres kezelések egyik fontos célja is ezen állapotromlások megelőzése. Az említett cikk két gyógyszert hasonlít össze: az egyik két szokványos hatóanyagot tartalmaz, a másik kiegészíti ezt egy harmadikkal, egy szteroiddal.

A kutatás egyik végpontja tehát az állapotromlások előfordulási gyakorisága volt; a hagyományos kezelést kapóknál 1,21 ilyen történt átlagosan egy évben, a tripla kombináció esetében ez lement 0,91-re.

Egyfelől tehát mondhatjuk, hogy az új gyógyszer kb. 25%-kal csökkenti az ilyen állapotromlások előfordulási gyakoriságát (relatív mutató), másrészt mondhatjuk, hogy évi 0,3 állapotromlást előz meg (abszolút mutató).

Első lépés: Nekünk a relatív mutató a lényeges eredmény a kísérletből. Ha a rendelőnkben épp velünk szemben ülő beteg esetében neme, életkora, társbetegségei stb. alapján mondjuk 2 állapotromlás várható évente a hagyományos kezeléssel, akkor arra számíthatunk, hogy ezt a gyógyszer átlagosan 1,5-re fogja csökkenti (elfogadva, hogy a relatív mutató állandó). Hiába volt tehát más a konkrét betegünk kockázata, a relatív mutató használata lehetővé tette, hogy rá nézve is következtetést tudjunk levonni.

Második lépés: A gyógyszer abszolút előnye tehát ennél a betegnél 0,5 állapotromlás megelőzése évente. Itt is célszerűbb áttérni a fordított mutatóra, és azt mondani, hogy 2 évnyi kezeléssel előzünk meg egy állapotromlást.

A kérdés tehát így már egyértelmű: megéri-e két éven át kezelni a beteget (két éven át tartó kezelés mellékhatásainak kitenni, két évnyi gyógyszert kifizettetni) azért, hogy egy állapotromlást megelőzzünk? Ez a kérdés természetesen nem dönthető el statisztikai úton – azon múlik, hogy egyrészt milyen súlyú az állapotromlás, másrészt milyen súlyúak a mellékhatások – de a statisztika segít abban, hogy világosan megfogalmazzuk, lássuk, és így jól meg tudjuk érteni, hogy egyáltalán mi a kérdés, milyen alternatívák között kell dönteni.

6.5 Különböző kimenetek közös nevezőre hozása

De mi az a másik terület, ahol jól jönnek az abszolút mutatók? Ez azonnal világos lesz, ha nem csak a főhatással, hanem a mellékhatásokkal is elkezdünk számolni. A tripla kombináció egyik problémája, hogy a szteroid-tartalma miatt megnöveli a tüdőgyulladás esélyét: a kísérlet eredményei szerint a dupla kombináció esetében évi átlag 0,061 ilyen fordult elő, de az új szernél már 0,096.

Mondhatjuk, hogy kb. 50%-kal megnöveli a tüdőgyulladás kockázatát, ami nagyon hasznos mutató, ha más betegre vagy betegcsoportra akarjuk vetíteni ezt, tehát a kutatásból tényleg ezt kell kiolvasni, ahogy láttuk is, de nem sokat segít az összehasonlításban! Vegyük ugyanis észre, hogy a „25%-kal csökkenti az állapotromlás kockázatát” és az „50%-kal növeli a tüdőgyulladás kockázatát” egymással totálisan összevethetetlen kijelentések! Miért? Azért, mert nagyon más a kiindulási alap! Állapotromlásból évi 1 fordul elő, tüdőgyulladásból tizedannyi (6.3. ábra).

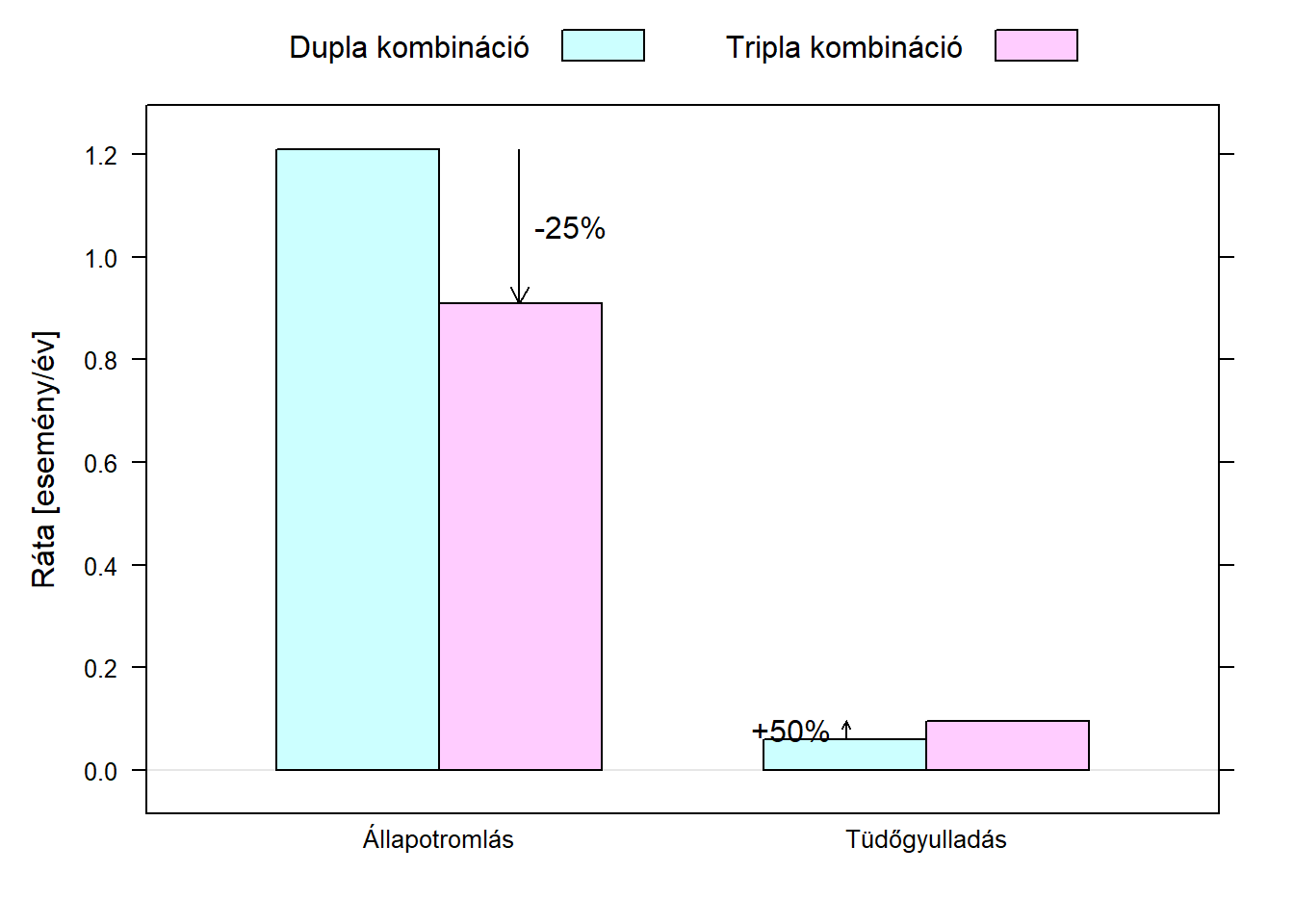
6.3. ábra. A kétféle végponton mért hatás nem összevethető, ha a hatást relatív mutatóval mérjük, mert teljesen más a kiindulópontjuk.

Itt jön az abszolút mutatók másik előnye: megteremtik az összehasonlíthatóságot! A példa kedvéért mondjuk, hogy a betegünk tüdőgyulladás-kockázata a régi kezeléssel 0,1 eset évente, akkor – elfogadva a relatív mutató stabilitását ebben is – az új kezelés mellett 0,15-re számíthatunk. A tripla kombináció tehát évi 0,05 tüdőgyulladást okozott, vagy – megint csak megfordítva a jobb érthetőség kedvéért – 20 évnyi kezeléssel okozunk mi, a gyógyszeradással egy többlet-tüdőgyulladást.

És akkor azonnal látható, hogy miért beszélhetünk az összehasonlíthatóság megteremtéséről: ha 2 év kezeléssel előzünk meg egy állapotromlást, de 20 év kezeléssel okozunk egy tüdőgyulladást, akkor egész egyszerűen azt mondhatjuk, hogy 10 állapotromlást előzünk meg 1 tüdőgyulladás okozása árán! (Az egyszerűség kedvéért vegyük úgy, hogy a gyógyszernek nincs más előnye mint az állapotromlás megelőzése és nincs más hátránya mint a tüdőgyulladás okozása.)

Megint csak: az természetesen nem statisztikai kérdés, hogy ez megéri-e, az azon múlik, hogy a tüdőgyulladás milyen súlyú az állapotromláshoz képest, de így legalább már látható, értelmesen, hogy egyáltalán mit kell összevetni – a relatív mutatókból ez nem derült ki!

6.6 Kitérő: patikamérlegen az emberélet

De tényleg nem statisztikai kérdés az előbbi? Talán nem tisztán az, de igenis lehet még szerepe a statisztikának, hogy segítsük az orvosi döntéshozatalt! Mondjuk, hogy egyetlen dologtól félünk mind az állapotromlás, mind a tüdőgyulladás kapcsán, ez pedig az, hogy a beteg belehal. (Sajnos csakugyan mindkettőbe bele lehet halni, pláne egy rosszabb állapotú COPD-s beteg esetén.) Ekkor igenis továbbvihető a dolog számszerűsítése: nézzük meg, hogy mekkora a halálozási kockázat az állapotromlás és mekkora a tüdőgyulladás esetén! A befejezés innentől már egyértelmű: ha az utóbbi kockázat kevesebb, mint tízszer akkora, akkor megéri az új gyógyszer, ha nem, akkor a régivel jár jobban a beteg.

Első hallásra kicsit ijesztő lehet, hogy ilyen szikár számokra fordítjuk le emberek életét, de valójában a statisztikai adatokkal explicite nem támogatott orvosi döntéshozatal is hajszálpontosan ugyanezeket a megfontolásokat alkalmazza, legfeljebb implicite – akkor viszont már jobb, ha explicitté tesszük!

A probléma sokkal inkább az, hogy a döntési helyzet nem ennyire „egydimenziós”. Nem csak arról van szó, hogy a gyógyszernek nem az állapotromlás megelőzése az egyetlen előnye és a tüdőgyulladás okozása az egyetlen hátránya, hanem arról is, hogy a kimeneteket nem lehet egyszerűen arra szűkíteni, hogy a beteg meghalt-e vagy sem. Ezzel ugyanis azt mondjuk, hogy mindenki, aki nem halt meg az pontosan ugyanolyan állapotban van: nincs különbség aközött, hogy makkegészséges vagy mondjuk ágyhoz kötött, önellátásra képtelen beteg.

A dolog kézenfekvő továbbfejlesztési lehetősége tehát az, hogy valamilyen formában ezt az ún. egészségi állapottal összefüggő életminőséget is figyelembe vesszük. Mondjuk ha valaki 10 évet nyer a gyógyszer hatására, de ágyhoz kötött betegként, az kevesebbet ér, mintha 10 tökéletes egészségben töltött évet nyerne. Ezek a megközelítések matematikai szemmel ugyan tetszetősek lehetnek, de etikailag nagyon problémásak. A legnagyobb gond, hogy valamilyen formában le kellene mérni azt, hogy a különböző életminőségek „mennyit érnek” a tökéletes egészséghez képest. Hány százalék életminőség romlás a tökéletes egészséghez képest az, ha vak vagyok? Ha süket? Ha ágyhoz között? Ha amputált? Ezekre a kérdésekre borzasztó nehéz válaszolni, és az is nagy kérdés, hogy van-e egyáltalán értelmük ilyen formában.

(Mindazonáltal kutatók intenzíven foglalkoznak ezekkel a problémákkal. Az egyik lehetőség, hogy megkérdeznek betegeket, hogy hány évnyi tökéletes egészségben töltött időre cserélnék le 10, adott állapotban töltött évüket. Ha 10-et mondanak, akkor tökéletes az életminőségük, ha 9-et, akkor 10% a betegségük életminőséget rontó hatása, ha 8-at akkor 20% és így tovább.)

6.7 Végpontok megválasztásának problémái

E kitérő után térjünk vissza a végpontokhoz, mert egy nagyon fontos kérdést még nem érintettünk. Eddig a lemérésről beszéltünk, de van egy alapvetőbb kérdés is: a végpont megválasztása! Ez első hallásra elég felesleges kérdésnek hangzik (mit kell ezen megválasztani? – az a végpont, ami érdekel minket!), de valójában ez sem ilyen egyszerű kérdés.

A legfontosabb probléma az, hogy sok esetben, ha szó szerint vesszük azt, hogy „ami érdekel minket” akkor olyan kísérlethez jutunk, amit lehetetlen, vagy nagyon nehéz végrehajtani. Vegyünk egy példát! Miért adunk vérnyomás-csökkentő gyógyszert a magas vérnyomású betegeknek? Azért, hogy csökkentsük a stroke-kockázatukat, csökkentsük az infarktus-kockázatukat és így tovább. Akkor tehát mi legyen a végpont egy vérnyomás-csökkentő gyógyszerjelölt vizsgálatában? Természetesen a stroke-rizikó, az infarktusrizikó, és így tovább.

Ez elmondva nagyon logikus, de valójában van egy hatalmas problémája, amiről már esett is sok szó: az, hogy rendkívül nehéz lesz kimérni kísérletben a hatást! Az infarktus, pláne a stroke nem fordul elő túl sűrűn, ezért vagy hatalmas mintanagyságra lenne szükség, vagy nagyon hosszú utánkövetésre (vagy leginkább mindkettőre…), és láttuk, hogy pont ez a kettő problémás egy kísérletben.

A megoldás tehát az lesz, hogy azt mérjük, hogy a vérnyomás-csökkentő csökkenti-e a vérnyomást. (Hiszen az nagyon rövid idő után kimérhető, és mindenkire kimérhető.) Ez így már-már mókásan egyértelműnek is tűnhet, de vegyük észre, hogy valójában van mögötte egy rendkívül fontos háttérfeltételezés: az, hogy a normalizált vérnyomás tényleg kisebb szív-érrendszeri kockázattal jár együtt! Ez viszont már egyáltalán nem nyilvánvaló, és ezen belül is különösen fontos az, hogy önmagában az a tény, hogy a normális vérnyomású embereknek kisebb a szív-érrendszeri rizikója még nem jelenti azt, hogy a vérnyomás mérése jó megoldás! Ha ez így lenne, akkor egy fogfehérítő készítmény könnyen hatásosnak bizonyulhatna a tüdőrák megelőzésére (gondoljuk végig!).

Az ilyen mutatókat, melyek kevesebb betegen, illetve hamarabb is kimérhetőek, ám közben jól mutatják, hogy milyen lenne a hatás a – csak sok betegen, illetve lassan kimérhető – valódi végponton, szokás helyettesítő végpontnak nevezni. Hiszen a betegnek nem lesz attól jobb, hogy egy műszer által kiírt szám valamilyen értéket mutat (a magas vérnyomás, kevés kivételtől eltekintve, önmagában semmilyen panaszt nem okoz), neki attól lesz jobb, ha nem kap infarktust. Fontos újra hangsúlyozni, hogy mindez csak akkor jogos, ha tényleg igaz, hogy a helyettesítő végpont a fenti értelemben jó, tehát, hogy a csökkenése tényleg maga után vonja – ha kevesebb beteget érintően és később is – az igazi végpont javulását.

Összefoglalva, a helyettesítő végpontok szerepe hatalmas, hiszen lehetővé teszik, hogy a gyógyszerek hatását könnyebben megítéljük, vagy egyáltalán, képesek legyünk megítélni. Azt is látni kell azonban, hogy a helyettesítő végpontok használata „veszélyes üzem”, épp az előbb tárgyalt feltétel miatt. Az ideális eset az, ha a betegség valódi végpontra gyakorolt hatása teljes egészében átmegy a helyettesítő végponton, és a vizsgált beavatkozás a betegség és a helyettesítő végpont között hat. Sajnos több történeti példát lehetne hozni arra, hogy nagyon logikusnak tűnő helyettesítő végpontok bizonyultak katasztrofálisan rossznak.

Az egyik leghíresebb eset a CAST kísérlet, melyben azt vizsgálták a ’80-as évek végén, hogy bizonyos kamrai szívritmuszavarokat megelőzni hivatott gyógyszerek (flekainid, enkainid és moracizin) hogyan hatnak a halálozásra infarktuson átesett betegek esetében. Az korábbról is ismert volt, hogy e gyógyszerek csakugyan csökkentik a kérdéses szívritmuszavarok előfordulását – márpedig az jól ismert, hogy ezek nagyban megnövelik a hirtelen szívhalál esélyét. A szívritmuszavar halálhoz vezethet, a gyógyszer megelőzi a szívritmuszavart, tehát a gyógyszer csökkenti a halálozási kockázatot. Tiszta sor, nem? Sajnos nem! A gyógyszereket törzskönyvezésük után évente 200 ezer beteg kezdte Amerikában szedni, mire az említett CAST kísérletben végre kiderült, hogy bár a ritmuszavarok előfordulását csakugyan csökkentik, de van velük egy apróbb probléma: a halálozást viszont megnövelik! A valószínűsíthető magyarázat, hogy az alapbetegség más úton is hat a hirtelen szívhalálra, nem csak a ritmuszavaron keresztül, és erre az útvonalra a gyógyszernek kimondottan rossz hatása volt. Kevesebb ritmuszavar, több halál – pedig ugye mennyire logikus volt az ellenkezője?

A helyettesítő végpontokkal tehát mindig óvatosnak kell lenni, és ellenőrizni kell, hogy a fenti feltételt teljesítik-e (szép szóval úgy szokták mondani: jól validált helyettesítő végpont-e).

6.8 Több végpont egyidejű vizsgálata

Mostanra alaposan kiveséztük a végpontok kérdését – azonban csak egyetlen végpontról beszélve! A valódi klinikai vizsgálatokban általában nem csak egyetlen kimenetel érdekel minket, az azonban további problémákat vet fel, ha több végpontot egyszerre kell figyelnünk.

Az egyetlen végpont összehasonlítása kapcsán megtárgyalt számos kérdésből egy dolgot érdemes most felidézni: azt, hogy a szokásos (bár számos szempontból kritizálható – néhányról már e hasábokon is volt szó) eljárás szerint úgy határozzuk meg, hogy mikor mondjuk, hogy egy hatás nem pusztán a véletlen műve, hogy igaz legyen, hogy ha valójában nincs hatás, akkor 5%-os valószínűséggel mondjuk mégis azt, tévesen, hogy van. (Miért 5% és nem kevesebb, ha egyszer mi mondjuk meg és ez egy tévedés valószínűsége? Lecsökkenthetnénk, de akkor megnőne annak a valószínűsége, hogy a valódi hatásokra is azt mondjuk, hogy csak a véletlen miatt vannak.) A szokásos szóhasználat szerint ilyenkor fogalmazunk úgy, hogy „szignifikáns” a hatás, kifejezve azt, hogy ilyenkor már nem hisszük – de nem kizárt! – hogy a hatás a véletlen miatt van. Hibázhatunk, de erre van szükség ahhoz, hogy egyáltalán bármit tudjunk mondani.

6.8.1 Vadászni mentünk… szignifikanciára

Ez az 5% ilyen értelmű hibavalószínűség remekül működik akkor, ha egyetlen végpontunk van. Bonyolódik azonban a helyzet akkor, ha több végpontot hasonlítunk és azokat „vagylagosan” kezeljük, tehát akkor kiáltunk fel, hogy találtunk valamit, ha bármelyik végpontban van eltérés. Mondjuk, hogy a gyógyszer hatását nem csak azzal mérjük le, hogy csökkenti-e a szívroham kockázatát, hanem azzal is, hogy csökkenti-e az agyvérzését. Külön-külön 5% a valószínűsége, hogy alaptalanul kiáltunk fel (tehát mondjuk, hogy az adott végponton hat a gyógyszer, miközben a valóságban nem is), de együtt már közel sem! Hiszen ezen hozzáállás mellett akkor is hibásan kiáltunk fel, ha vagy az egyik, vagy a másik végponton hibásan kiáltunk fel; ennek valószínűsége természetesen összekombinálódik a külön-külön vett tévedések valószínűségéből. Mintha lenne két húszoldalú, szabályos dobókockánk, és azt kérdeznénk, hogy mekkora a valószínűsége, hogy a kettőből valamelyik 1-est dob – ami értelemszerűen nagyobb, mint, hogy bármelyikkel külön 1-est dobunk (ami 5% ebben a példában). Nem a két 5% összege, ahogy azt sokan gondolnák elsőre, a matematika ennél egy nagyon kicsit bonyolultabb, de most ez nem különösebben érdekes, a végeredmény: 9,75%.

Az orvosi példánkra visszatérve mindez azt jelenti, hogy bár mi azt hirdetjük magunkról, hogy 5%-on vizsgálódtunk, azaz a téves találat (nem hat a gyógyszer de mi mégis azt mondjuk, hogy igen) valószínűsége 5%, a valóságban e vagylagos hozzáállás mellett az ilyen tévedés valószínűsége ennek majdnem kétszerese lesz! Ahogy nő a végpontok száma a helyzet csak egyre romlik, ezt mutatja az 6.4. ábra. Érdemes úgy is ránézni a kérdésre, hogy az 5% azt jelenti, hogy ha sehol nincsen semmilyen hatás, akkor is várhatóan minden 20. esetben mégis találunk. Avagy: aki keres, az talál – csak itt ez nem feltétlenül jó hír…

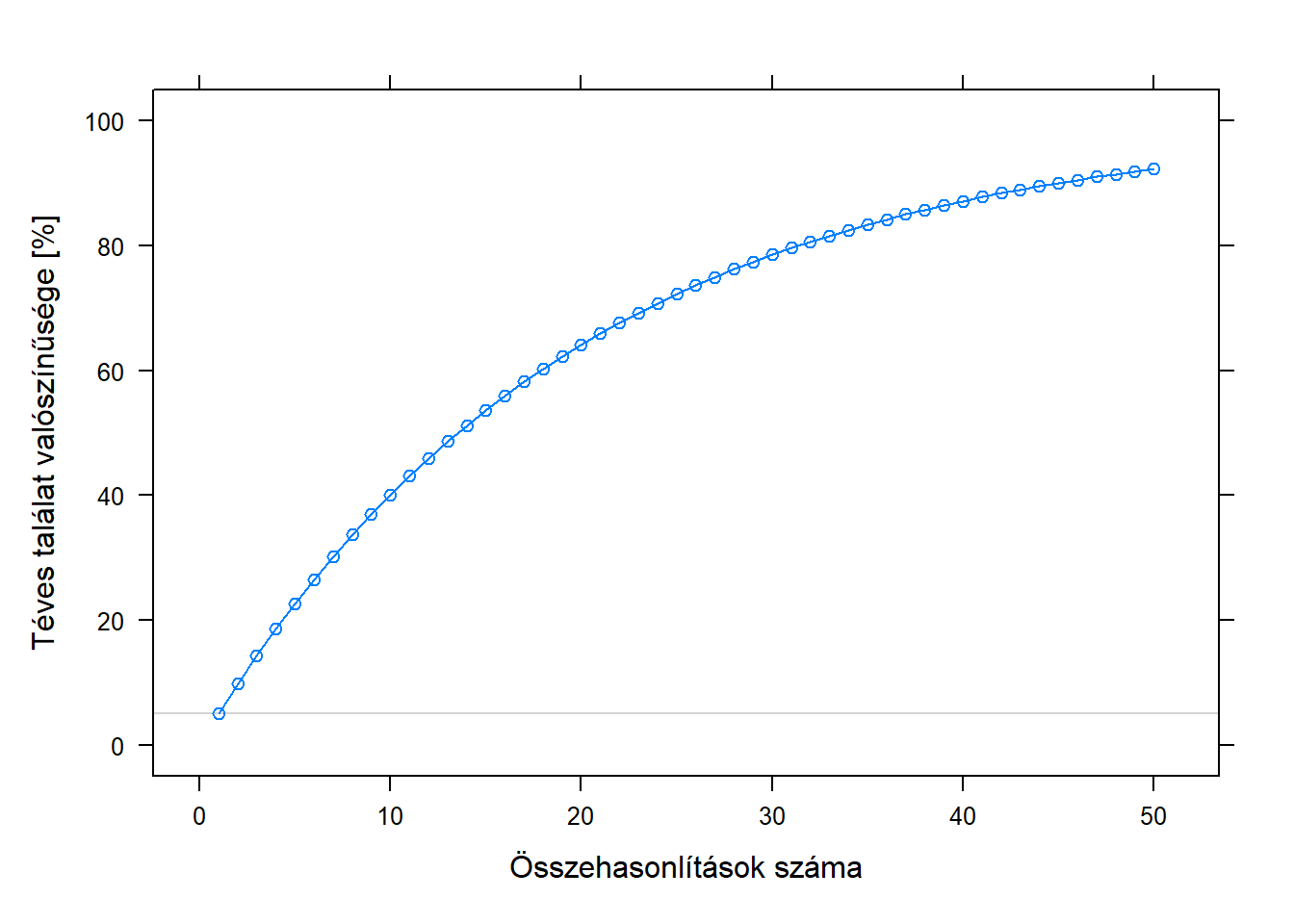
6.4. ábra. Adott számú végpont vagylagos összehasonlítása esetén annak a valószínűsége, hogy legalább egy tévesen hatást mutat, ha valójában semelyik végponton nincsen hatás (és a különböző végpontok függetlenek egymástól). A halvány szürke vonal az 5%-ot mutatja, mely az egyes összehasonlítások külön-külön vett ilyen hibavalószínűsége.

A problémakör e ponton kettéágazik. Az egyik irány a nyílt rosszhiszeműség: addig növelni az összehasonlítások számát, amíg valahol csak találunk valamit. Például be akarjuk bizonyítani, hogy az emberek vére szisztematikusan eltér aszerint, hogy hosszú-e a vezetéknevük. Ez első ránézésre elég megmosolyogtatónak hangzik, pedig valójában pofonegyszerűen bizonyítható! Semmi más dolgunk nincs mint fogni 100-100 rövid és hosszú vezetéknevű embert és egy teljesen rutin laborvizsgálatnak alávetni őket. Manapság ezek is 20, 30, vagy akár ennél is több paramétert mérnek le, ha ezeket mind összehasonlítjuk egyesével, akkor elég nyugodtan hátradőlhetünk, hogy legalább egy különbséget találni fogunk (lásd 1. ábra!).

Innentől két lehetőségünk van. Az egyik, hogy leírjuk a cikkben, hogy 30 összehasonlítást végeztünk, ebből 29 esetben nem találtunk szignifikáns különbséget, 1 esetben igen. Ebből minden olvasó tudni fogja, hogy mit találtunk: semmit, hiszen az az 1 különbség tökéletesen megfelel annak, amennyit akkor várunk, a véletlen ingadozásnak köszönhetően, ha semmiben nincs különbség. Igen ám, csakhogy. Van egy másik lehetőség is: „megfeledkezünk” róla, hogy mi valójában 30 dolgot hasonlítottunk össze, kitalálunk utólag egy filozófiát ahhoz az 1-hez, és úgy írjuk le, mintha eleve is, célirányosan azt néztünk volna meg. Mondjuk egy gyulladásmarkerben találunk eltérést, akkor úgy írjuk meg a cikket, hogy van egy fantasztikus kórélettani teóriánk, miszerint a hosszú vezetéknevű embereket frusztrálja, hogy olyan lassú amíg aláírják a papírokat, és ez a frusztráció egy szervezetszintű gyulladást hoz létre bennük – éppen ezért célirányosan megmértük egy gyulladásos paraméterüket, és láss csodát, tényleg eltér. (Tételezzük fel, hogy nincs confounding, tehát nem lehet, hogy valami összefügg a vezetéknévvel, ami hat a gyulladásra is.) Az igazán nagy baj ebben az, hogy az ilyen típusú csalást magából a cikkből nem lehet lebuktatni! Hiszen ha tényleg célirányosan csak a gyulladásmarkert vizsgáltuk volna meg, akkor teljesen rendben is lenne ez az eredmény. Ami természetesen nem azt jelenti, hogy biztosan igaz lenne, de tényleg 5% lenne ennek az eredménynek a valószínűsége akkor, ha valójában nem lenne különbség. (Ami természetesen, emlékezzünk vissza a korábbi írásokra, nem ugyanaz, mint hogy 5% valószínűséggel nincs különbség!) Persze, ha a megdöbbentő eredményen fellelkesülve egy másik kutatócsoport megpróbálja reprodukálni a vizsgálatunkat, akkor jó eséllyel lebukunk; egész pontosan csak 5% a valószínűsége, természetesen, hogy – véletlenből kifolyólag – ők is ugyanezt találják.

Számos csalás vagy félreértés megy ugyanerre a kaptafára; ezt szokás, meglehetősen találó kifejezéssel, szignifikanciavadászatnak nevezni az irodalomban. Nézzünk egy másik példát!

Ez a jelenség természetesen nem csak több végpont esetén fordulhat elő – a kritérium az, hogy több összehasonlítást hajtsunk végre (nem véletlen az 6.4. ábrán a tengely felirata!), ezért szokás egyébként ezt többszörös összehasonlítások problémájának nevezni. Ez lehet több végpont összehasonlítása, de lehet több kezelés összehasonlítása ugyanazon a végponton, vagy egy kezelés összehasonlítása egy végponton, de több csoportban. Ez utóbbihoz tekintsük a következő kijelentést: „a gyógyszer 5%-os szignifikanciaszinten szignifikáns hatással bír a 30-40 év közötti cukorbeteg férfiak körében”. Rendben van ez így? Az őszinte válasz erre a kérdésre, hogy nem tudjuk! Ha csakugyan célirányosan a 30-40 év közötti cukorbeteg férfiakat vonták be a vizsgálatba, akkor minden rendben, legalábbis ebből a szempontból. (Ami persze nem azt jelenti, hogy biztosan igaz az állítás, és még csak azt sem, hogy 5% a tévedés, azaz a gyógyszer hatástalanságának a valószínűsége, ezt nem lehet elégszer hangsúlyozni.) Azonban enyhén szólva is erős lehet a gyanúnk, hogy erről szó sincs, hanem egyszerűen nem hatott a gyógyszer, ezért elkezdtek próbálkozni. Esetleg csak a férfiakban? Csak a nőkben? Csak a cukorbetegekben? Ha ezt a fenti módon, kombinatorikusan tesszük, akkor nagyon hamar rengeteg összehasonlításunk lesz (10 korcsoporttal, 2 nemmel és 2 cukorbetegség szerinti állapottal számolva 40!), ami pontosan ugyanahhoz a problémához vezet mint a vezetékneves példa.

6.8.2 Egy nem csak biostatisztikai tanulságokkal bíró kitérő

A szignifikanciavadászatra sok példát lehetne hozni; az alábbi azért érdekes, mert a szignifikanciavadászaton (sőt, általában a statisztikai kérdéseken) messze túlmutató tanulságokkal is bír. A történet eredetileg nem a szignifikancia-vadászatra van kihegyezve, hanem az újságírók alaposságát akarta megvizsgálni, de a sztori magvában, mint majd látni fogjuk, a szignifikancia-vadászat van.

2015-ben egy Johannes Bohannon nevű szerző és munkatársai, a német Táplálkozási és Egészségügyi Intézet kutatói, közöltek egy tanulmányt az International Archives of Medicine nevű orvosi lapban, ami nagyon leegyszerűsítve arról szólt, hogy a csokoládéevés segít a fogyásban. Egy rendes klinikai kísérletről volt szó, empirikusan vizsgálták meg a kérdést: az alanyokat véletlenszerűen több csoportra osztották, és azt találták, hogy a csokoládét evő csoport testtömege szignifikánsan csökkent a kontrollokéhoz viszonyítva. Gyönyörű grafikonok, táblázatok, \(p\)-értékek, részletes diszkusszió az eredményekhez, számos irodalmi hivatkozással, ahogy kell.

A tanulmánnyal azonban van pár apróbb probléma. Az egyik, hogy „Táplálkozási és Egészségügyi Intézet” nem létezik, a másik, hogy „Johannes Bohannon” nevű kutató nem létezik (más intézetben sem, ez ugyanis álnév, a szerző igazi neve John Bohannan, és valójában angol tudományos újságíró, nem német orvos), a harmadik, hogy a folyóirat egy jól ismert kamu lap. (Kitérő a kitérőben: a tudományos folyóiratok klasszikus modelljével szemben, melynél az olvasó fizet a lap vagy cikk elolvasásáért, egy új modell is kialakult, melyben a cikkek ingyen elolvashatóak, cserében viszont a szerzőknek kell fizetniük a megjelenésért. Ez sok szempontból pozitív és rendkívül szimpatikus kezdeményezés, azonban sajnos létrejött egy erre rátelepedő csalási iparág is. Ebben a „folyóiratok” valójában semmilyen bírálatot nem alkalmaznak, akármit közölnek – néha szó szerint akármit, véletlenszerűen egymás után rakott szavakból álló cikket is… – majd begyűjtik a pénzt a szerzőktől a közlésért. Bárki, aki valaha írt igazi tudományos cikket, tudja miről van szó, ugyanis a postaládájába naponta tízesével érkezik a levélszemét az ilyen „folyóiratoktól”… Az International Archives of Medicine egy ilyen lap; ez amúgy nagyon gyorsan ki is deríthető róla.)

Összefoglalva, egy nem létező intézet nem létező kutatója közzétesz egy cikket egy kamu folyóiratban, amely cikk ráadásul módszertanilag is botrányos (erről majd picit később); és a kérdés: vajon mi fog történni? Hányan veszik ezt észre? A válasz: újságok, tévék, internetes portálok, beleértve egészségügyi rovatokat, sőt, magukat a táplálkozástudományban jártasnak mondó szerzők, százával vették át a hírt az egész világon, egyetlen újságíró nem akadt, aki utánanézett volna, hogy mit is közöl. Amiben az az igazán kétségbeejtő, hogy nem kéthetes kutatómunkára lett volna szükség a dolog felderítéséhez: Bohannonék minden lehetségeset megtettek, hogy a lehető legkönnyebben lebukjanak. Ha beüti valaki az intézet nevét a Google-be, kiderült volna, hogy sehol nincs nyoma sem, a weboldalát akkor hozták létre, ha beütik a kutató nevét bármelyik tudományos adatbázisba, kiderült volna, hogy nem is létezik. 30 másodperc munka, ha lassan végzik, 2 perc. És akkor arról még nem beszéltünk, hogy esetleg, netalántán, mielőtt egy ilyen cikk konklúzióját változtatás nélkül közlik, talán meg lehetne kérdezni egy hozzáértőt, hogy maga a cikk amúgy rendben van-e módszertani szempontból. De nem, senki nem akadt, aki ezt megtette volna, sőt, a bulvárlapok még fokozták is a hírt („miért kell [!] minden nap csokoládét enned”)… A helyzet odáig fajult, hogy végül Bohannon-nak saját magát kellett lebuktatnia egy cikkben, hogy megállítsák a dolgot. Jusson ez eszünkbe, ha kedvenc lapunkban legközelebb az épp aktuális új tudományos világszenzációról olvasunk…

Na de mi köze ennek az egésznek a szignifikancia-vadászathoz? A helyzet az, hogy a szerző kamu, az intézet kamu, a folyóirat kamu, de egy dolog valódi volt: a kutatás! Bármilyen meglepő, az nem volt kamu, Bohannonék tényleg verbuváltak kísérleti alanyokat, tényleg véletlenszerűen csoportba osztották őket, tényleg etettek velük csokit (vagy sem) és tényleg lemérték, hogy mi történik velük. És a testtömegük tényleg csökkent!

Ez tehát igaz, csak épp – és most jön a lényeg – valójában 18 különböző dolgot mértek le, egyáltalán nem csak a testtömeget! Az tehát, hogy találtak 1 különbséget, tökéletesen megfelel annak, hogy semmiben nincsen semmilyen különbség. A nem statisztikai tanulságra visszatérve, az igazán szomorú az, hogy – szemben a vezetékneves példával – ezt meg sem próbálták eltitkolni, épp ellenkezőleg, teljesen világosan leírták, hogy 18 összehasonlítást végeztek. Tehát még a módszertani hibát sem lett volna nehéz megtalálni (a többihez hasonlóan, mert nem ez volt az egyetlen!) – ennek ellenére vették át a hírt a különféle lapok, internetes oldalak, rendkívül lehangoló képet festve arról, hogy mennyire működik valójában a kritikus szemlélet. Sajnos ez nem csak a laikus sajtóra igaz…

(Záró megjegyzésként fontos ugyanazt a figyelmeztetést hozzátenni, mint a confounding esetében: ez nem azt jelenti, hogy akkor cáfoltuk, hogy a csokoládé-evés fogyasztana – éppenséggel fogyaszthat is, csak épp ez a tanulmány ezt rettenetesen kevéssé bizonyítja.)

6.8.3 A jóhiszemű kutatók nehézségei

Bizonyos értelemben a fenti még a jobbik eset. Ez ugyanis direkt csalás, joggal mondhatjuk, hogy ilyet nem lehet véletlenül csinálni, és így a jóhiszemű kutatóknak nem kell aggódniuk. A probléma, mint sok más esetben, akkor jelentkezik, amikor az ilyen többszörös összehasonlításoknak teljesen legitim okai vannak. A vezetékneves példa lehet, hogy abszurd, de mi van, ha egy betegségnél mi sem tudjuk, hogy melyik laborváltozóban okoz eltérést, és ezt akarjuk kideríteni? Mi van, ha egy környezeti hatás esetében több száz betegségről szeretnénk kideríteni, hogy valamelyiknek növeli-e a kockázatát?

A legjobb példa minderre talán az alcsoport-elemzések intézménye. Alcsoport-elemzés alatt azt értik az orvosi irodalomban, amikor egy vizsgálat végén az egész elemzést megismétlik úgy, hogy az adatokat leszűkítik különböző csoportokra. Hogyan hat a gyógyszer csak a férfiakban és csak a nőkben? Cukorbetegekben és nem cukorbetegekben? Idősekben és fiatalokban?

Itt is az a nehéz helyzet, amikor nem rosszhiszeműen járunk el, mint az írás elején felhozott hasonló példában, hanem tényleg kíváncsiak vagyunk erre, mert elvileg tényleg lehet, hogy a gyógyszer bizonyos csoportokban nem hat (vagy csak bizonyos csoportokban hat). Ezért az alcsoport-elemzéseknek van létjogosultságuk, de hogy legalábbis óvatosan kell velük bánni, arra az irodalom egyik legszórakoztatóbb példáját egy 1988-as kutatás hozta. Ezt ma már minden bizonnyal nem így neveznék el – annak idején ugyanis az ISIS-2 nevet kapta… Ez a kísérlet azt vizsgálta, hogy 3 kezelési stratégia (egy sztreptokináznak nevezett vérrögoldó adása, aszpirin adása, vagy mindkettő adása egyszerre) hogyan hat infarktusban a halálozás megelőzésére. A 6.5. ábra mutatja az eredményeket. Az alsó kettő meglehetősen szokásos alcsoport-analízis: a cukorbetegekben nem hat a gyógyszer (a nem cukorbetegekben igen), az infarktuson átesettekben nem hat a gyógyszer (a korábban infarktust el nem szenvedőknél igen). Ha csak az ábra jobb oldalát nézzük, akkor a legfelső pár is nagyon hasonló ezekhez, de nézzük csak meg jobban a feliratot a bal oldalon! A legfelső alcsoport-analízis tárgya, hogy a betegnek mi a csillagjegye – az eredmények szerint Ikrek és Mérleg jegyűekben nem hat a gyógyszer, a többiekben igen…

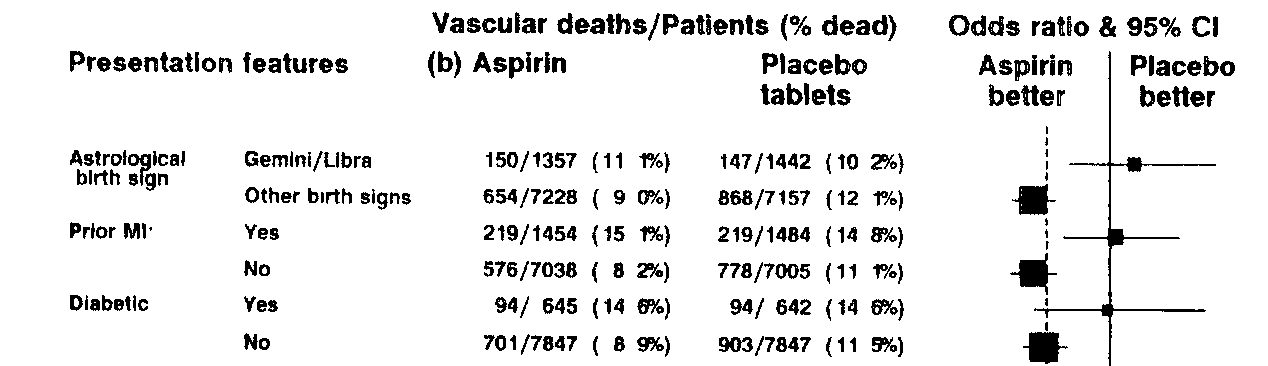
6.5. ábra. Kissé meglepő eredmények az aszpirin hatására vonatkozóan: facsimile oldal az ISIS-2 vizsgálat közleményéből. A jobb oldalon lévő folytonos függőleges vonal a „hatástalanság vonala”, amelyik csoport vízszintes vonala metszi, ott az adott csoportban nem hat a gyógyszer. A csoportok fentről lefelé: csillagjegy (Ikrek/Mérleg, egyéb), korábbi infarktus (igen, nem), cukorbeteg (igen, nem).

A megállapítás, amelyet ez a példa nagyon szellemesen szemléltet, hogy a cukorbetegség és a csillagjegy között az egyetlen különbség, hogy az előbbihez jobb filozófiát tudnak kitalálni az orvosok, hogy ott miért nem hat a gyógyszer, az utóbbihoz meg talán picit kevésbé… De az eredmények statisztikai bizonyítóereje pontosan ugyanaz mindkét esetben!

Mi akkor a megoldás mindezen problémákra? A kérdés összetett, itt talán csak elég két pontot kiemelni. Az egyik, hogy bizonyos esetekben nem akarjuk megoldani a problémát. Az alcsoport-elemzéseknél sokszor ez a helyzet: a cikkek nem próbálják meg statisztikai úton helyrerakni a dolgot, cserében viszont ekkor az alcsoport-elemzések eredményét nem lehet bizonyítékként kezelni (legfeljebb felvetésként: ha valahol gyanús eltérést látunk, akkor azt rendes vizsgálatban célirányosan meg kell nézni, de az alcsoport-analízis önmagában nem bizonyít, csak felveti a gyanút).

Máskor szeretnénk korrigálni a többszörös összehasonlítások helyzetét; a jó hír, hogy erre vannak módszerek. Az alkalmazásuk kapcsán sok vita van, de az fontos, hogy egyáltalán lehet a problémán statisztikai úton segíteni. Vegyük például a következő ötletet. Mi a probléma alapja? Az, hogy hiába rakjuk 5%-ra a szintet összehasonlításonként, összességében ez meg fog nőni, ahogy azt az 6.4. ábra is mutatja, jóval 5% fölé. Akkor mit csináljunk? Vegyük le a szintet összehasonlításonként, hogy összességében kapjunk 5%-ot! Bebizonyítható matematikai úton példának okáért, hogy ha az összehasonlításonkénti szintet úgy állítjuk be, hogy az 5%-ot elosztjuk az összehasonlítások számával (tehát például 10 összehasonlítás esetén 0,5%-ra rakjuk), akkor az összességében vett hibavalószínűség – annak a valószínűsége, hogy téves módon hatást mutatunk ki bárhol, miközben igazából sehol nincs hatás – nem lehet több mint 5%. A módszer neve Bonferroni-korrekció, az eredményét a 6.6. ábra szemlélteti.

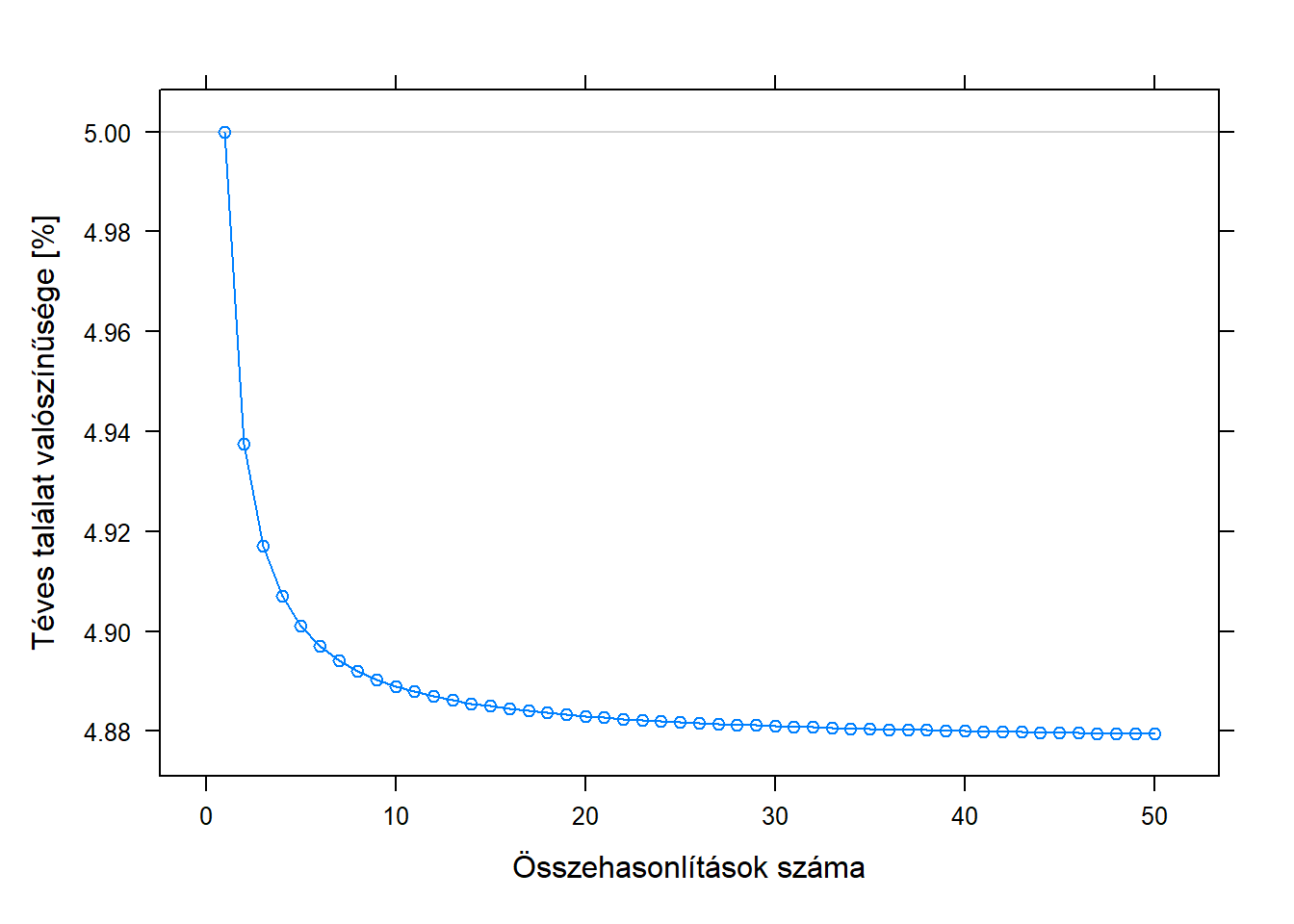
6.6. ábra. A Bonferroni korrekció hatása: az alaphelyzet ugyanaz, mint az 1. ábra esetében, de az összehasonlításonkénti szignifikanciaszintet lecsökkentettük, annyiadrészére ahány összehasonlítást végeztünk. Jól látszik az eredmény: a téves találat valószínűsége igen pontosan 5% marad (illetve soha nem megy fölé), akárhány összehasonlítást is végzünk.

A Bonferroni-korrekciónak nagyon sok baja van (például rendkívül szigorú, nagyon megnehezíti a valódi hatások észrevételét is – azaz nagyon lecsökkenti az erőt), de azt jól szemlélteti, hogy a probléma kezelhető statisztikai úton.