5. fejezet Néhány további témakör a gyógyszervizsgálatok témájából
5.1 Több végpont használata, többszörös összehasonlítások helyzete
A statisztikai szignifikanciánál láttuk, hogy a szokásos 5%-os szignifikanciaszint használata azt jelenti, hogy ha nincsen hatás, mi 5% valószínűséggel fogunk mégis, a véletlen ingadozás miatti pech miatt, tévesen hatást kimutatni. (És láttuk, hogy ezt a szintet csökkenteni sem feltétlenül érdemes, hiszen akkor meg a valódi hatások detektálását is megnehezítjük.) Ez teljesen rendben is van akkor, ha egyféle hatást vizsgálunk meg. De mi történik akkor, ha több összehasonlítást végzünk? Ennek talán legkézenfekvőbb példája, amikor több végpontot vizsgálunk, például azt is megnézzük, hogy a gyógyszer az infarktus előfordulását csökkenti-e, és azt is, hogy a stroke előfordulását csökkenti-e.
Külön-külön vizsgálódva nincsen semmi különös: ha a gyógyszer egyikre sem hat, akkor 5% valószínűséggel fogunk mégis hatást kimutatni mindkettő esetében. Ha azonban azt kérdezzük, hogy mekkora valószínűséggel fogunk legalább az egyiknél tévesen hatást kimutatni, az máris rögtön nagyobb lesz, mint 5%! Gondoljunk bele, a dolog úgy is felfogható, hogy van egy cinkelt pénzérménk, ami 5% valószínűséggel mutat fejet feldobásnál. Ekkor annak a valószínűsége, hogy egy dobásból fejet kapunk 5%, de annak a valószínűsége, hogy két dobásból legalább egy fejet kapunk, nyilván jóval nagyobb. Az meg pláne, hogy 10-ből dobunk legalább egy fejet. Ha tehát „vagylagosan” vizsgálódunk, azaz akkor mondjuk, hogy találtunk valamit, ha bármelyik összehasonlításnál (pl. bármelyik végponton) találunk hatást, akkor óvatosan kell eljárni.
Ez egy példa a többszörös összehasonlítások helyzetének nevezett általános jelenségre, ami akkor lép fel, ha a fenti értelemben „vagylagosan” végzünk több vizsgálatot (Schulz és Grimes 2005). Az érzékeltetés kedvéért, a következő ábra mutatja pontosan kiszámolva4 annak valószínűségét, hogy valahol (legalább egy összehasonlításban) találunk hatást, ha valójában sehol nincs hatás, annak függvényében, hogy hány összehasonlítást végeztünk:
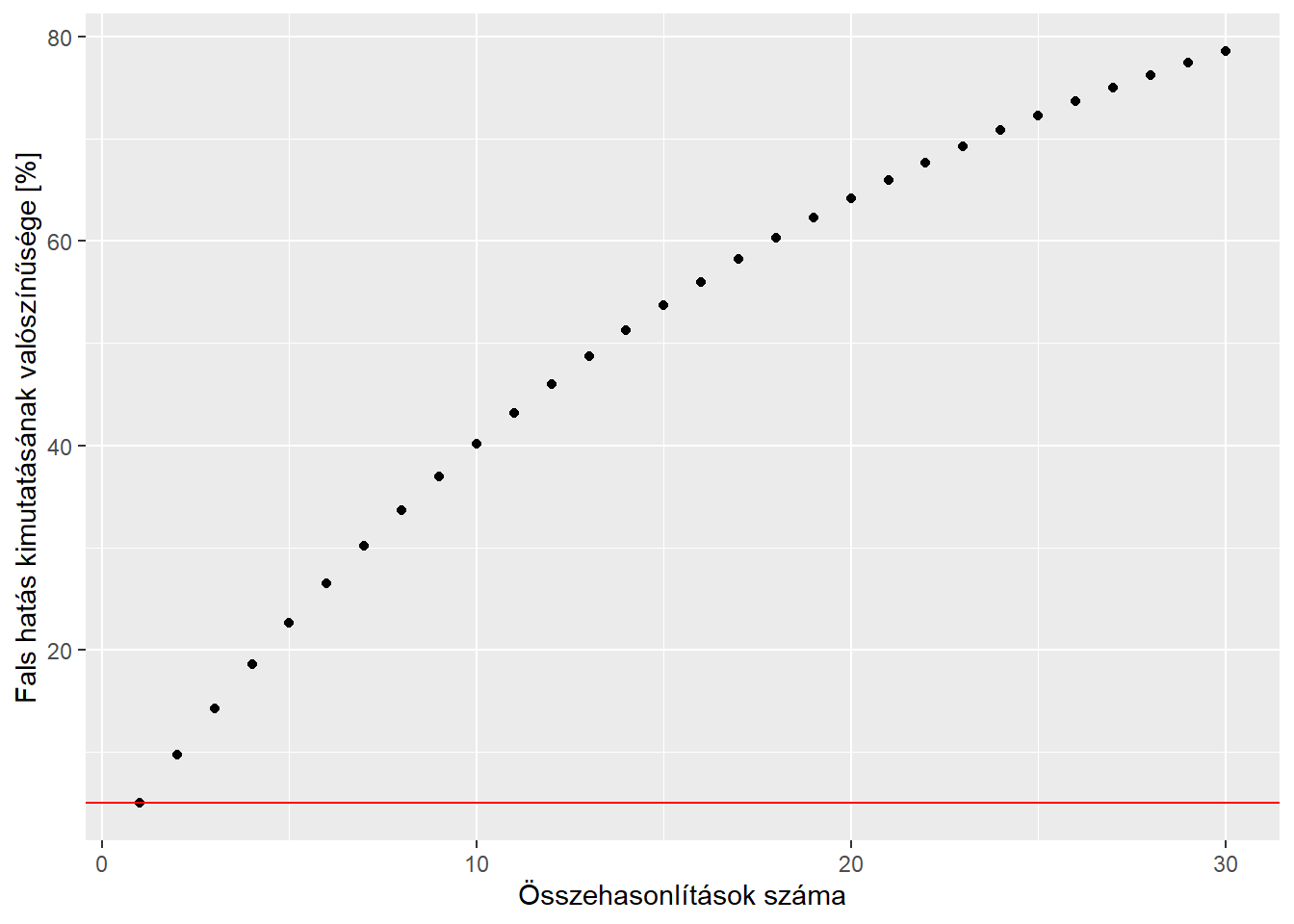
A ábrán piros vonallal jelölt 5% a szignifikanciaszint: egy összehasonlításnál tényleg rendben van minden, és ez lesz a fals találat valószínűsége, de látható, hogy az összehasonlítások számának emelkedésével – ahogy éreztük is – gyorsan nő ez a valószínűség.
A több végponton kívül van még pár eset, ami valójában ugyanerre a problémára vezet, például ha több betegcsoportban is megvizsgáljuk a gyógyszer hatását vagy ha több időpontban is megvizsgáljuk a gyógyszer hatását (ezekkel fogunk foglalkozni a következő pontokban), de az alapprobléma mindenhol ugyanaz: ha több összehasonlítást végzünk, megnő annak a valószínűsége, hogy tévesen hatást mutatunk ki. Ilyenkor szükség lehet arra, hogy megfelelő statisztikai korrekciókat tegyünk. Ezeknek számos módszere van, pusztán az érzékeltetés kedvéért, az egyik ilyen lehetőség, hogy az egyes vizsgálatok szignifikanciaszintjét csökkentjük. Hiszen a jelenség az volt, hogy a „fals találat” valószínűsége megnő ahhoz képest, mint az egyes összehasonlítások szignifikanciaszintje – akkor csökkentsük le ez utóbbit, hogy még a megnövekedés után is annyi legyen, ami számunkra elfogadható, például 5%!
5.2 Alcsoport-analízis
Bizonyos esetekben felmerül a lehetőség, hogy egy gyógyszer hatása valamilyen meghatározott csoportban, például adott nemben, életkorban, genetikai szempontból, valamilyen társbetegség mellett, a betegség súlyossága, vagy épp a terápia megkezdésének időpontja szerint eltér. Hogyan lehet ezt megvizsgálni?
Kézenfekvő lehetőség, hogy szűkítsük le az adatainkat a vizsgált csoportra, például vegyük ki csak a férfiakat a mintából, és számoljuk ki az eredményt az ő körükben. A gyakorlatban általában úgy járnak el, hogy ilyen esetben mindegyik csoportra – a példánál maradva: férfiakra és nőkre is – kiszámolják az eredményeket, és egymás mellett közlik. Természetesen több szempont szerinti csoportosítást is vizsgálhatunk. Ezt az eljárást szokás alcsoport-analízisnek hívni.
A módszer nagyon csábító, hiszen rendkívül egyszerű, és mégis megválaszolhatja sok kérdésünket arról, hogy egy bizonyos csoportban külön hogyan hat a gyógyszer – valójában azonban számos csapdája van (Sleight 2000; Schulz és Grimes 2005; Assmann és mtsai. 2000; Yusuf és mtsai. 1991).
Az még csak a kisebbik baj, hogy ha leszűkítjük a vizsgált betegek körét, akkor kisebb lesz a beteglétszám, így a véletlen ingadozás megnő, a becslések bizonytalanabbak lesznek, azaz kisebb lesz a statisztikai erő. Ennek egyik következménye, hogy fals módon mondhatjuk azt, hogy adott alcsoportban nincs hatás, holott akár még az is lehet, hogy a hatás pontosan ugyanakkora abban az alcsoportban is, mint az egész vizsgálatban, csak épp a kevesebb beteg miatt erről nem tudjuk igazolni, hogy szignifikáns. A nagyobb probléma, hogy alcsoportból nagyon sok tud lenni, és ez végképp igaz, ha kombináljuk is őket (pl. cukorbeteg, 60-70 éves férfiak alcsoportja). Azaz: az imént tárgyalt többszörös összehasonlítási helyzettel állunk szemben! Az összehasonlítások száma most az alcsoportok száma, és a következtetés ugyanaz: nagyon gyorsan megnő annak a valószínűsége, hogy legalább egy alcsoportban akkor is találunk hatást, ha sehol nincsen! Ez a két probléma ráadásul némiképp még fel is erősíti egymást, hiszen ahogy korábban láttuk, a túl kis erő pedig ahhoz fog vezetni, hogy ha téves hatást találunk, annak a mérete ráadásul még nagy is lesz.
Mindezeken némileg segít, ha limitált az alcsoportok száma, az pedig különösen fontos, hogy előre eldöntött legyen, hogy milyen alcsoportok kerülnek elemzésre, mert a legveszélyesebb az, ha ezt az adatok alapján, az eredményeket nézegetve találják ki a kutatók (így nagyon nagy lesz a valószínűsége, hogy olyan alcsoportot találnak, ami csak abban a konkrét mintában mutat eltérést). Tökéletes megoldást azonban ezek sem jelentenek.
Akkor mire jók mégis az alcsoport-analízisek? Mivel elképzelhető, hogy a gyógyszer hatása tényleg eltér bizonyos alcsoportokban, és ezt fontos is lenne felderíteni, így nem lehet egyszerűen figyelmen kívül hagyni ezt a témakört. Fontos azonban, hogy az alcsoport-analízisek eredményei mindig óvatosan kezelendőek, és jellegük szerint inkább csak felvetik a lehetőségét, hogy egy alcsoport máshogy viselkedik, de önmagukban nem bizonyítják. Ezért a valóban releváns feltevéseket később megerősítő jellegű vizsgálatokban célirányosan igazolni kell.
5.3 Interim elemzések, korai leállítás
A gyógyszervizsgálatokról eddig elmondottakból úgy tűnhet, hogy ha egy maszkolt vizsgálatról van szó, akkor egészen a vizsgálat lezárásáig senki nem tudhatja, hogy melyik beteg tartozott a kezelt, és melyik a kontrollcsoportba. Ez elméletben tényleg így is van, de gyakorlatilag nem kivitelezhető, és nem csak azért, mert valakinek be kell csomagolnia a szereket kívülről nézve azonos csomagolásba. Bele kell nézni menet közben is az adatokba, minimum a biztonság miatt (ha valami bajt okoz a szer, azt muszáj hamar észrevenni), de akár a hatásosság miatt is: ha találunk egy nagyon hatásos készítményt, akkor sem szerencsés, ha hónapok, adott esetben évek múlva derül csak ki.
A megoldást az jelenti, hogy létezik egy, a kutatást végzőktől természetesen szigorúan független – hogy a maszkolás fennmaradjon – bizottság, amelynek tagjai belenézhetnek menet közben is az eredményekbe. Értékelhetik azokat, és ez alapján szükség esetén a független bizottság határozhat a vizsgálat korai leállításáról, de az egyéb módosításokról is. Az ilyen, menet közben végzett kiértékelést szokták interim analízisnek nevezni.
A fenti elmondásból az egész nagyon sima ügynek tűnhet, pedig valójában itt is vannak csapdák. A legfontosabb probléma, hogy minden egyes „belekukucskálás” az eredményekbe egy lehetőség, hogy szignifikáns hatást kapjunk akkor is, ha nincs hatás! Minél többször tesszük meg, annál nagyobb a valószínűsége, hogy fals módon hatást mutatunk ki – ez tehát pontosan ugyanaz a probléma, amit a többszörös összehasonlítások esetén láttunk; az összehasonlítások száma itt a menet közbeni kiértékelések száma.
Mivel azonban fontos, hogy mégis tudjunk interim analízist végezni, ezért számos módszert találtak ki, amit alkalmazni lehet, hogy korrekt eredményt kapjunk5.
Amíg a biztonság miatti leállítás szerepét senki nem kérdőjelezi meg, addig a hatásosság miatti leállítás gyakran vált ki vitákat a szakirodalomban. A módszertani problémákon túl egy fontos etikai megfontolás is szerepet játszik ebben: bár „matematikailag” mindegy, hogy valaki azért hal meg, mert súlyos mellékhatást szenved el egy nem jó gyógyszertől, vagy pedig azért, mert nem jut hozzá időben egy jó gyógyszerhez, az orvosok számára ez a kettő nem ugyanaz – sokkal nagyobb súllyal esik latba az a kár, amit az aktív tevékenységükkel okoztak. Ezt fejezi ki igazából a „nil nocere” – „ne árts” – elve (nem azt, hogy semmit nem szabad tenni a beteggel, ami elvileg akár árthat is neki, mert akkor semmilyen orvosi beavatkozást nem lehetne soha senkin végezni).
5.4 A gyógyszervizsgálatok fázisai
Itt nem célunk a gyógyszervizsgálatok szervezésével kapcsolatos milliónyi – és a gyakorlatban fontos – technikai kérdésre kitérni, de egy dolgot megemlítünk, mert ez gyakran előkerül a közbeszédben is.
A gyógyszerfejlesztés folyamatának azon első lépéseit, amikor a gyógyszert még nem adják embernek, preklinikai fázisnak szokás nevezni. Ide tartoznak a számítógépes modellezések, a laboratóriumban sejtkultúrákon és szöveteken végzett vizsgálatok, az állatkísérletek stb. Ha egy gyógyszerjelölt e fázison átmegy és ígéretesnek tűnik, akkor jön az emberi kipróbálás szakasza, amit klinikai fázisnak szoktak nevezni. A preklinikai fázisban ugyan megpróbálják kizárni a kockázatokat (és maximalizálni annak a valószínűségét, hogy hatásos legyen a gyógyszer), de ez igazán biztosan csak akkor dől el, ha ténylegesen embernek adják a vizsgált készítményt. Ebből adódóan a klinikai fázis a gyógyszerfejlesztés legkritikusabb, és ezzel összhangban a legjobban szabályozott területe. Számos szomorú történelmi példa után ma már klinikai vizsgálatban kizárólag önkéntesek vehetnek részt.
A klinikai szakaszt általában három fázisra szokták bontani. Az 1-es fázisú vizsgálatok során néhány kivételtől eltekintve a gyógyszert kislétszámú (jellemzően néhány tucatnyi) és általában teljesen egészséges alanynak adják. Ebből is rögtön látható, hogy ekkor még nem kell gyógyítania a gyógyszernek! Akkor mi szükség van erre a fázisra? A válasz az, hogy itt ismerik meg a kutatók azt, hogy a gyógyszernek mi a sorsa az emberi szervezeten belül (hogyan szívódik fel, hogy oszlik szét a szervezetben, hogyan alakul át, hogyan távozik), hogy a szervezetben hogyan fejt ki hatást, ez milyen mutatókkal írható le, hogy ezek összefüggenek-e a szervezeten belüli viselkedés mutatóival. Általában az 1-es fázis során különböző dózisokat adnak be, hogy megtalálják, hogy melyik lehet az optimális. Bár hatásosságot itt még nem néznek, de biztonságot nagyon is: nyomon követik a mellékhatásokat, ez is segít annak kiválasztásában, hogy mely dózisok jöhetnek szóba a későbbi vizsgálatokhoz.
A 2-es fázis kritikus lépés: itt kell először gyógyítania is a gyógyszernek. A 2-es fázisú vizsgálatokban a gyógyszerjelöltet már betegeknek adják, de egyébként jó állapotban lévő és nem túl nagy létszámú (jellemzően 100 körüli vagy alatti), rendkívül megválogatott és nagyon szorosan monitorozott csoportnak. Itt is rögzítik ugyanúgy a biztonsági végpontokat, de itt először vizsgálják a hatásosságot is. A cél még nem ennek a pontos felmérése, csak annak eldöntése, hogy egyáltalán a remény megvan-e arra, hogy a gyógyszer működjön, azaz van-e megfelelő dózis, aminél a kockázat-haszon mérleg kellő betegcsoport számára pozitív lehet. Szükség esetén tovább optimalizálják, és itt véglegesítik az adagolást is.
Ha igen, akkor a gyógyszerjelölt továbblép az utolsó, legnagyobb volumenű, és legkomplexebb szakaszba. A 3-as fázis során a készítményt már nagy létszámú (akár több ezer fős) betegcsoportnak adják, nagyon gyakran számos vizsgálóhelyen, a betegeket jóval kevésbé megválogatva, ezzel is közelítve a való életbeli helyzethez. Amellett, hogy ugyanúgy nyomon követik itt is a biztonsági végpontokat, ez lesz a perdöntő információforrás a hatásosság megítéléséhez, a korábbi feltételezések megerősítéséhez. A gyógyszerjelölt akkor kaphat törzskönyvet, ha ezen a fázison is sikeresen átjut.
Manapság a 3-as fázisú vizsgálatok nagyon kevés, jól megindokolt kivételtől eltekintve mind randomizált, kontrollált kutatások.
Szoktak néha még 4-es fázisú vizsgálatokról is beszélni. Ez a kifejezés némileg kakukktojás, mert ez már nem a gyógyszerfejlesztési folyamat része, hanem a törzskönyvezés utáni fázisé. A kutatómunka ugyanis nem ér véget a törzskönyvezéssel és a forgalomba hozatallal: bármilyen nagy létszámú is volt a fázis 3 vizsgálat, gyakran előfordul, hogy vannak kérdések, amik eldöntéséhez még ez is kevés. Ahogy láttuk, a kis hatások megítéléséhez – legyen szó akár kis főhatásról, akár ritka mellékhatásról – nagy mintanagyság kell; nagyon kis hatáshoz akkora mintanagyság is szükséges lehet, ami a fázis 3 vizsgálatban sem érhető el. Ezeket csak akkor lehet tanulmányozni, amikor a gyógyszer már széleskörű alkalmazásba került; van rá példa, hogy ilyenkor már több százezer beteg bevonásával készítenek kutatásokat. Az ilyen vizsgálatok további célja, hogy információt gyűjtsön a való életbeli hatásról, hiszen még a 3-as fázis betegei is általában sok szempont (életkor, társbetegségek stb.) szerint válogatott körből származnak, a betegminta összetétele eltér az összes betegétől. Cserében a dolog kevésbé lehet szigorúan szabályozott, mint a 3-as fázisban; itt már nagyon sokszor kerül sor megfigyeléses vizsgálatok végzésére is.
5.5 A bizonyítékok összessége szemlélet
Az orvosi kérdések eldöntésekor – és ez alól természetesen a gyógyszerek hatásosságának a megítélése sem kivétel – soha nem az a kérdés, hogy egy konkrét vizsgálat mit mutat, hanem az, hogy mi a teljes tudásunk az adott témakörben. Ez adott esetben állhat egyetlen vizsgálatból, állhat többől is, ez utóbbi esetben a különböző kutatások bizonyító ereje eltérő is lehet.
Éppen ezért fontos, hogy egy kérdés megválaszolását lehetőleg a teljes, rendelkezésre álló tudásunkra alapozzuk. Ez a gyakorlatban két feladat megoldását igényli: a tudást tartalmazó közlemények valamilyen módon történő összegyűjtését (review), lehetőleg reprodukálható módon (szisztematikus review), és a közleményekből kiolvasható eredmények megfelelő statisztikai módszerrel történő aggregálását (meta-analízis). A statisztikai módszerekre azért van szükség, mert itt nem lehet egyszerűen átlagolni: minden részlet nélkül, ha egy 20 fős vizsgálat azt találta, hogy a halálozási arány 10%, egy 1000 fős pedig azt, hogy 20%, akkor érezhető, hogy nem lehet azt mondani, hogy együtt azt mondják, hogy a válasz 15%. Valahogy tehát a kutatások bizonytalanságát is figyelembe kell venni, erre szolgálnak a meta-analízis módszerei.
Fontos hangsúlyozni, hogy a meta-analízisre csak akkor van szükség, ha nem ismerjük a vizsgálatokban résztvevő betegek adatait személy szerint, egyénileg. Ha igen, akkor csak „össze kell önteni őket” (persze pár dologra még ekkor is figyelni kell, de ez már részletkérdés), de a gyakorlatban elég tipikus helyzet, hogy az egyéni eredményeket nem, csak az összesítést ismerjük. Például nem tudjuk az egyedi vérnyomás értékeket, csak az átlagukat és a szórásukat. Ez a tipikus helyzet akkor, ha a nyers adatokhoz nem férünk hozzá, csak a kutatásról készült publikációt tudjuk elolvasni. Ilyenkor van szükség a meta-analízis eszköztárára.
Végezetül nagyon fontos rögzíteni, hogy a meta-analízis sem jelent csodafegyvert: eleve limitálja, hogy csak aggregált adatok alapján tud dolgozni, és ha a bemenő adatok mind rossz minőségűek, akkor abból nem lesz varázslatosan jó minőségű eredmény semmilyen módszerrel sem.
Egyedül annyit kellett a számításhoz feltételeznünk, hogy az egyes összehasonlítások egymástól függetlenek.↩︎
Ezek helyenként egészen komplexek, de az alapgondolat általában az, amit a többszörös összehasonlításoknál is láttunk: belenézhetünk többször is, de akkor szigorúbbnak kell lennünk, hogy a végén összességében is megőrizzük az 5%-os fals hatás-kimutatás valószínűséget.↩︎